
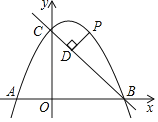
【题目】如图,直线y=﹣x+4与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且OA=![]() OB,抛物线y=ax2+bx+4经过A,B,C三点.
OB,抛物线y=ax2+bx+4经过A,B,C三点.
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上的动点,设点P的横坐标为m,过点P作PD⊥BC,垂足为D,用含m的代数式表示线段PD的长,并求出线段PD的最大值.
【答案】(1)y=﹣![]() x2+x+4;(2)PD=﹣
x2+x+4;(2)PD=﹣![]() (m﹣2)2+
(m﹣2)2+![]() ,,PD有最大值,最大值为
,,PD有最大值,最大值为![]() .
.
【解析】
(1)先求出点A、B的坐标,再利用待定系数法求解即可;
(2)先求出C、P的坐标,由此得到线段CP的长度,根据平行线的性质得![]() ,解直角三角形即可求出PD的表达式,利用二次函数的性质求出PD的最大值即可.
,解直角三角形即可求出PD的表达式,利用二次函数的性质求出PD的最大值即可.
(1)在y=﹣x+4中,当x=0时,y=4;当y=0时,x=4,
∴B(4,0),C(0,4),
∴OB=OC=4,
∴OA=![]() OB=2,
OB=2,
即A(﹣2,0),
把A(﹣2,0),B(4,0)代入y=ax2+bx+4中,得
![]() ,解得
,解得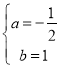 ,
,
抛物线的解析式为:y=﹣![]() x2+x+4;
x2+x+4;
(2)过P作PF∥y轴,交BC于F,
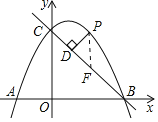
在Rt△OBC中,∵OB=OC=4,∴∠OCB=45°,
∴∠PFD=45°,
∴PD=![]() PF,
PF,
由P(m,﹣![]() m2+m+4),F(m,-m+4),得:PF=﹣
m2+m+4),F(m,-m+4),得:PF=﹣![]() m2+2m,
m2+2m,
∴PD=![]() (﹣
(﹣![]() m2+2m)
m2+2m)
=﹣![]() (m﹣2)2+
(m﹣2)2+![]() ,其中,0<m<4,
,其中,0<m<4,
∵﹣![]() <0,
<0,
∴当m=2时,PD有最大值,最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
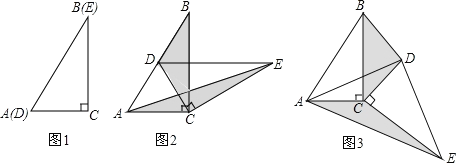
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC统点C旋转到点D恰好落在AB边上时,如图2.
①当∠B=∠E=30°时,此时旋转角的大小为 ;
②当∠B=∠E=α时,此时旋转角的大小为 (用含a的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
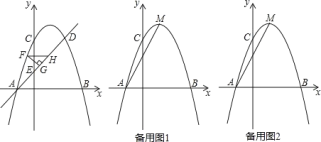
【题目】如图,抛物线 y=﹣x2+bx+c 与 x 轴交于 A、B 两点,与 y 轴交于点 C ,点 A 的坐标为(-1,0),点 C 的坐标为(0,3),点D和点 C 关于抛物线的对称轴对称,直线 AD 与 y 轴交于点 E .
(1)求抛物线的解析式;
(2)如图,直线 AD 上方的抛物线上有一点 F,过点 F 作 FG⊥AD 于点 G,作 FH 平行于 x 轴交直线 AD 于点 H,求△FGH 周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
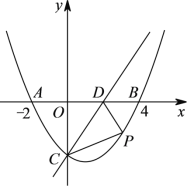
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0),B(4,0),与直线![]() 交于点C(0,-3),直线
交于点C(0,-3),直线![]() 与x轴交于点D.
与x轴交于点D.
(1)求该抛物线的解析式.
(2)点P是抛物线上第四象限上的一个动点,连接PC,PD,当△PCD的面积最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了销售一种新型“吸水拖把”,对销售情况作了调查,结果发现每月销售量y(只)与销售单价x(元)满足一次函数关系,所调查的部分数据如表:(已知每只进价为10元,销售单价为整数,每只利润=销售单价﹣进价)
销售单价x(元) | 20 | 22 | 25 | … |
月销售额y(只) | 300 | 280 | 250 | … |
(1)求出y与x之间的函数表达式
(2)该新型“吸水拖把”每月的总利润为w(元),求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,
FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )

A.1∶3 B.2∶3 C.![]() ∶2 D.
∶2 D.![]() ∶3
∶3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com