
【题目】河西王府井销售一种 T 恤衫,每件进价为 40 元,经过市场调查,一周的销售量y 件与销售单价 x 元/件满足某种函数关系:
销售单价 x (元/件) | 50 | 60 | 70 | 80 | ||
一周的销售量 y(件) | 350 | 300 | 250 | 200 |
(1)请根据所学的知识,选择合适的函数模型,求出 y 与 x 的之间的函数关系式;
(2)设一周的销售利润为 w 元,请求出 w 与 x 的函数关系式,并确定当销售单价为多少时一周的销售利润最大,并求出最大利润;
(3)商场决定将一周销售 T 恤衫的利润全部捐给某村用于精准扶贫的水网改造项目,在商场购进该T 恤衫的资金不超过 6000 元情况下,请求出该商场最大捐款数额是多少元?
【答案】(1) y=5x+600;(2)当销售单价为80元时一周的销售利润最大,最大利润为8000元;(3) 7500元,
【解析】
(1)利用待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析式,将其配方成顶点式,依据二次函数的性质可得答案;
(3)根据“商场购进该T恤衫的资金不超过6000元”知y≤![]() ,即-5x+600≤150,解之求得x的范围,结合二次函数的顶点式及其增减性可得.
,即-5x+600≤150,解之求得x的范围,结合二次函数的顶点式及其增减性可得.
解答
解:(1)设y=kx+b,
根据题意,得![]()
解得![]()
所以,y=5x+600;
(2)根据题意,得:w=(x40)(5x+600)=5x2+800x24000=5(x80)2+8000,
∵5<0,
∴当x=80时,w取得最大值,最大值为8000,
答:当销售单价为80元时一周的销售利润最大,最大利润为8000元;
(3)∵商场购进该T恤衫的资金不超过6000元,
∴y6000÷40,即5x+600150,
解得:x90,
∵w=5(x80)2+8000中,当x>80时w随x的增大而减小,
∴当x=90时,w取得最大值,最大值为7500,
答:该商场最大捐款数额是7500元.


科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:
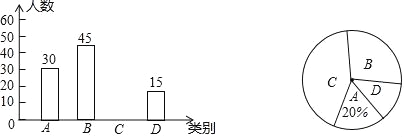
(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在边AB上,点F在边CD上,如果添加一个条件,使△ADE≌△CBF,那么添加的条件不能为( )

A.DE=BFB.AE=CFC.BE=DFD.∠ADE=∠CBF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.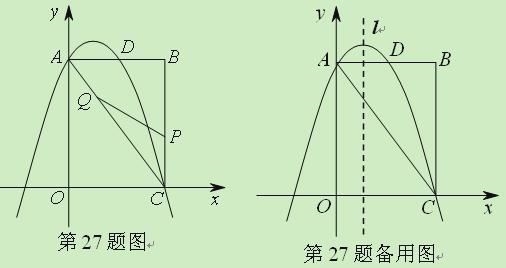
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.
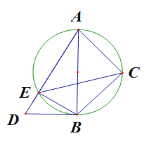
(1)求证:EC平分∠AEB;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
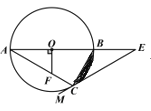
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,BC=![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司2月份销售新上市一种新型低能耗汽车20辆,由于该型汽车的优越的经济适用性,销量快速上升,4月份该公司销售该型汽车达到45辆,并且2月到3月和3月到4月两次的增长率相同.
(1)求该公司销售该型汽车每次的增长率;
(2)若该型汽车每辆的盈利为2万元,则平均每天可售10辆,为了尽量减少库存,汽车销售公司决定采取适当的降价措施,经调查发现,每辆汽车每降5000元,公司平均每天可多售出2辆,若汽车销售公司每天要获利14万元,每辆车需降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com