练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知A，B两地相距200千米，一辆汽车以每小时60千米的速度从A地匀速驶往B地，到达B地后不再行驶，设汽车行驶的时间为x小时，汽车与B地的距离为y千米．

    （1）求y与x的函数关系，并写出自变量x的取值范围；

    （2）当汽车行驶了2小时时，求汽车距B地有多少千米？


    解：（1）y=200﹣60x（0≤x≤）；

    （2）将x=2代入函数关系式得：y=200﹣60×2=80千米．

    答：汽车距离B地80千米．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图13，已知Rt△ACB中，∠C＝90°，∠BAC＝45°．

                            

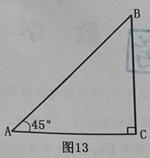
    （1）（4分）用尺规作图，：在CA的延长线上截取AD＝AB，并连接BD（不写作法，保留作图痕迹）

    （2）（4分）求∠BDC的度数．

    （3）（4分）定义：在直角三角形中，一个锐角A的邻边与对边的比叫做∠A的余切，记作cotA，即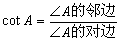，根据定义，利用图形求cot22.5°的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗，每次随机摸出一颗珠子，放回摇匀后再摸，通过多次试验发现摸到白珠子的频率稳定在0.3左右，则盒子中黑珠子可能有　　颗．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列一元二次方程中，没有实数根的是（　　）

    　   A．4x2﹣5x+2=0    B． x2﹣6x+9=0           C．                             5x2﹣4x﹣1=0  D． 3x2﹣4x+1=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点A，B，C是⊙O上的点，OA=AB，则∠C的度数为　　．

    30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与x轴相交于A，B两点，与y轴相交于点C，直线y=kx+n（k≠0）经过B，C两点，已知A（1，0），C（0，3），且BC=5．

    （1）分别求直线BC和抛物线的解析式（关系式）；

    （2）在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    设x1，x2是方程x2+5x﹣3=0的两个根，则x12+x22的值是（　　）

    　 A． 19 B． 25 C． 31 D． 30

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若|a﹣1|=a﹣1，则a的取值范围是（　　）

    　 A． a≥1 B． a≤1 C． a＜1 D． a＞1

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，线段AB是⊙O的直径，点C在圆上，∠AOC=80°，点P是线段AB延长线上的一动点，连接PC，则∠APC的度数是　　　　　　度（写出一个即可）．

    查看答案和解析>>

    同步练习册答案