
如图13,已知Rt△ACB中,∠C=90°,∠BAC=45°.
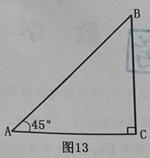
(1)(4分)用尺规作图,:在CA的延长线上截取AD=AB,并连接BD(不写作法,保留作图痕迹)
(2)(4分)求∠BDC的度数.
(3)(4分)定义:在直角三角形中,一个锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即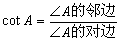 ,根据定义,利用图形求cot22.5°的值.
,根据定义,利用图形求cot22.5°的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
遵义市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题:

(1)参加调查测试的学生为 人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩中的中位数落在 组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图11,已知, l1∥l2,C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上,设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
|
| A. | 转化思想 |
|
| B. | 三角形的两边之和大于第三边 |
|
| C. | 两点之间,线段最短 |
|
| D. | 三角形的一个外角大于与它不相邻的任意一个内角 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com