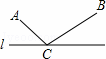
如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是（ ）
|
| A． | 转化思想 |
|
| B． | 三角形的两边之和大于第三边 |
|
| C． | 两点之间，线段最短 |
|
| D． | 三角形的一个外角大于与它不相邻的任意一个内角 |
A加金题 系列答案
全优测试卷系列答案科目：初中数学 来源： 题型：
如图，在Rt△ABC中，∠ABC= 90°，以AB为直径的⊙O与AC边交与点D．过D作⊙O的切线交BC与点E．连接OE.
(1)证明：OE∥AC；
(2)①当∠BAC= °时，四边形ODEB是正方形；
②当∠BAC= °时，AD=3DE.
查看答案和解析>>
科目：初中数学 来源： 题型：
如图13，已知Rt△ACB中，∠C＝90°，∠BAC＝45°．
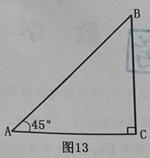
（1）（4分）用尺规作图，：在CA的延长线上截取AD＝AB，并连接BD（不写作法，保留作图痕迹）
（2）（4分）求∠BDC的度数．
（3）（4分）定义：在直角三角形中，一个锐角A的邻边与对边的比叫做∠A的余切，记作cotA，即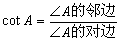
，根据定义，利用图形求cot22.5°的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
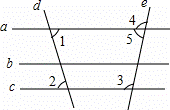
如图，下列说法错误的是（ ）
|
| A． | 若a∥b，b∥c， 则a∥c | B． | 若∠1=∠2，则a∥c |
|
| C． | 若∠3=∠2，则b∥c | D． | 若∠3+∠5=180°，则a∥c |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12米，那么该古城墙的高度是 米（平面镜的厚度忽略不计）．
查看答案和解析>>
科目：初中数学 来源： 题型：
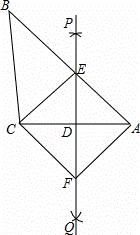
如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF．
（1）求证：△AED≌△CFD；
（2）求证：四边形AECF是菱形．
（3）若AD=3，AE=5，则菱形A
ECF的面积是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗，每次随机摸出一颗珠子，放回摇匀后再摸，通过多次试验发现摸到白珠子的频率稳定在0.3左右，则盒子中黑珠子可能有 颗．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的点在数轴上表示时，所在哪两个字母之间（ ）