练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图11，已知， l1∥l2，C1在l1上，并且C1A⊥l2，A为垂足，C2，C3是l1上任意两点，点B在l2上，设△ABC1的面积为S1，△ABC2的面积为S2，△ABC3的面积为S3，小颖认为S1＝S2＝S3，请帮小颖说明理由．


    解：∵直线l1∥l2，

    ∴△ABC1，△ABC2，△ABC3的底边AB上的高相等，

    ∴△ABC1，△ABC2，△ABC3这3个三角形同底，等高，

    ∴△ABC1，△ABC2，△ABC3这些三角形的面积相等．

    即S1=S2=S3．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


        问题提出

    如图①，已知直线l与线段AB平行，试只用直尺作出AB的中点．

    初步探索

    如图②，在直线l的上方取一个点E，连接EA、EB，分别与l交于点M、N，连接MB、NA，交于点D，再连接ED并延长交AB于点C，则C就是线段AB 的中点．

    推理验证

    利用图形相似的知识，我们可以推理验证AC＝CB．

    （1）若线段a、b、c、d长度均不为0，则由下列比例式中，一定可以得出b＝d的是（）

    A． ＝

    B．＝

    C．＝

    D．＝

    （2）由MN∥AB，可以推出△EFN∽△ECB，△EMN∽△EAB，△MND∽△BAD，

    △FND∽△CAD．

         所以，有＝＝＝＝，

             所以，AC＝CB．

    拓展研究

    如图③，△ABC中，D是BC的中点，点P在AB上．

    （3）在图③中只用直尺作直线l∥BC．

    （4）求证：l∥BC．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在圆心角为90°的扇形OAB中，半径OA=2cm，C为的中点，D、E分别是OA、OB的中点，则图中阴影部分的面积为　　　　　　cm2．

    　

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3，表示的点在数轴上表示时，所在哪两个字母之间（　　）

    A．C与D      B．A与B      C．A与C      D．B与C

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    词所指的物品         2

    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图13，已知Rt△ACB中，∠C＝90°，∠BAC＝45°．

                            

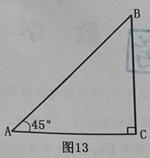
    （1）（4分）用尺规作图，：在CA的延长线上截取AD＝AB，并连接BD（不写作法，保留作图痕迹）

    （2）（4分）求∠BDC的度数．

    （3）（4分）定义：在直角三角形中，一个锐角A的邻边与对边的比叫做∠A的余切，记作cotA，即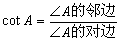，根据定义，利用图形求cot22.5°的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，下列说法错误的是（　　）

    　

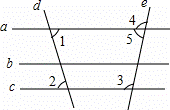
    A．

    若a∥b，b∥c，     则a∥c

    B．

    若∠1=∠2，则a∥c

    　

    C．

    若∠3=∠2，则b∥c

    D．

    若∠3+∠5=180°，则a∥c

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


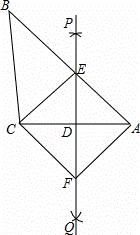
    如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF．

    （1）求证：△AED≌△CFD；

    （2）求证：四边形AECF是菱形．

    （3）若AD=3，AE=5，则菱形AECF的面积是多少？

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点A，B，C是⊙O上的点，OA=AB，则∠C的度数为　　．

    30°

    查看答案和解析>>

    同步练习册答案