
【题目】如图,在ABCD中,E、F分别是AD、BC的中点,BE、DF分别交AC于点G、H,连接DG、BH.
(1)求证:四边形EBFD是平行四边形;
(2)四边形GBHD是平行四边形吗?请说明理由;
(3)若GD=CH,试判断AC与GH之间的数量关系,并说明理由.
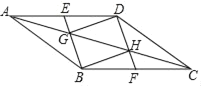
【答案】(1)详见解析;(2)是,证明详见解析;(3)AC=3GH,理由详见解析
【解析】
(1)根据一组对边平行且相等的四边形是平行四边形即可判断;
(2)根据(1)中结论,可得AD=BC,AD∥BC,BE∥DF,从而证明△ADH≌△CBG,再根据一组对边平行且相等的四边形是平行四边形即可;
(3)先证明△AEG∽△CBG,得出相似比,从而得到AC=3AG及AH=2CH,进而得出AC与GH的数量关系.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,DE∥BF,
∵E、F分别是AD、BC中点,
∴DE=BF,
∴四边形EBFD是平行四边形;
(2)解:∵四边形EBFD是平行四边形,
∴AD=BC,AD∥BC,BE∥DF,
∴∠DAH=∠BCG,∠AHD=∠CGB,
在△ADH与△CBG中, ,
,
∴△ADH≌△CBG(AAS),
∴DH=BG,
∵DH∥BG,
∴四边形GBHD是平行四边形;
(3)解:AC与GH之间的数量关系为:AC=3GH,
理由如下:
∵四边形ABCD是平行四边形,E、F分别是AD、BC的中点,
∴BC=AD=2AE,AE∥BC,
∴△AEG∽△CBG,
∴![]() ,
,
∴CG=2AG,
∴AC=3AG,即AG=![]() AC,
AC,
同理可得:AH=2CH,
∴AC=3CH,即CH=![]() AC,
AC,
∴GH=![]() AC,
AC,
即AC=3GH.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为____
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为____

查看答案和解析>>
科目:初中数学 来源: 题型:
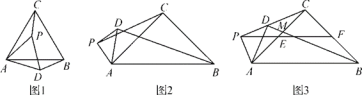
【题目】在△ABC中,CA=CB,∠ACB=α.点P 是平面内不与点A,C 重合的任意一点,连接AP,将线段AP 绕点P 逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)猜想观察:如图1,当α=60°时,![]() 的值是________,直线BD与直线CP相交所成的较小角的度数是________.
的值是________,直线BD与直线CP相交所成的较小角的度数是________.
(2)类比探究:如图2,当α=90°时,请写出![]() 的值及直线BD与直线CP相交所成的较小角的度数,并就图2的情形说明理由.
的值及直线BD与直线CP相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题:如图3,当α=90°时,若点 E,F 分别是 CA,CB 的中点,点 P 在FE的延长线上,P,D,C三点在同一直线上,AC与BD相交于点M,DM=2-![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一张锐角三角形的硬纸片.AD是边BC上的高,BC=40cm,AD=30cm.从这张硬纸片剪下一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.
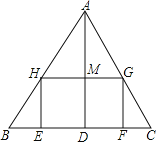
(1)求证:![]() ;
;
(2)求这个矩形EFGH的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走.
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数解析式(不要求写出自变量的取值范围);
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的条件下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
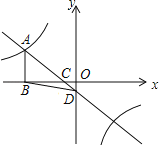
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(1)求一次函数和反比例函数的解析式;
(2)若直线AC与y轴交于点D,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
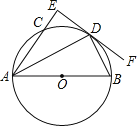
【题目】如图,在⊙O中,AB是直径,点C是圆上一点,点D是弧BC中点,过点D作⊙O切线DF,连接AC并延长交DF于点E.
(1)求证:AE⊥EF;
(2)若圆的半径为5,BD=6 求AE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
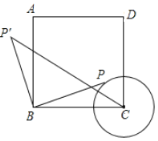
【题目】如图,正方形![]() 中,
中,![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径画
长为半径画![]() ,点
,点![]() 在
在![]() 上移动,连接
上移动,连接![]() ,并将
,并将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() .在点
.在点![]() 移动的过程中,
移动的过程中,![]() 长度的最小值是( )
长度的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com