
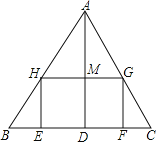
【题目】如图,△ABC是一张锐角三角形的硬纸片.AD是边BC上的高,BC=40cm,AD=30cm.从这张硬纸片剪下一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.
(1)求证:![]() ;
;
(2)求这个矩形EFGH的周长.
【答案】(1)证明见解析;(2)72cm.
【解析】
(1)根据矩形性质得出∠AHG=∠ABC,再证明△AHG∽△ABC,即可得出结论;
(2)根据(1)中比例式即可求出HE的长度,以及矩形的周长.
解:(1)证明:∵四边形EFGH为矩形,
∴EF∥GH,
∴∠AHG=∠ABC,
又∵∠HAG=∠BAC,
∴△AHG∽△ABC,
∴![]() ;
;
(2)解:由(1)![]() 得:设HE=xcm,则MD=HE=xcm.
得:设HE=xcm,则MD=HE=xcm.
∵AD=30cm,
∴AM=(30﹣x)cm.
∵HG=2HE,
∴HG=(2x)cm,
可得:![]() ,
,
解得:x=12,
故HG=2x=24,
所以矩形EFGH的周长为:2×(12+24)=72(cm).
答:矩形EFGH的周长为72cm.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是第一象限内横坐标为![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是______.
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
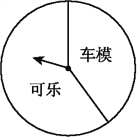
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产化肥的总任务一定,平均每天化肥产量y(吨)与完成生产任务所需要的时间x(天)之间成反比例关系,如果每天生产化肥125吨,那么完成总任务需要7天.
(1)求y关于x的函数表达式,并指出比例系数;
(2)若要5天完成总任务,则每天产量应达到多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
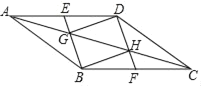
【题目】如图,在ABCD中,E、F分别是AD、BC的中点,BE、DF分别交AC于点G、H,连接DG、BH.
(1)求证:四边形EBFD是平行四边形;
(2)四边形GBHD是平行四边形吗?请说明理由;
(3)若GD=CH,试判断AC与GH之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
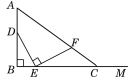
【题目】如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=![]() DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
A.-![]() B.-
B.-![]() C.-
C.-![]() D.-
D.-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com