
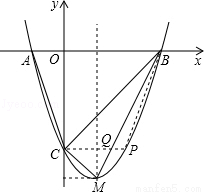
(12分)如图,抛物线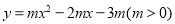 与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
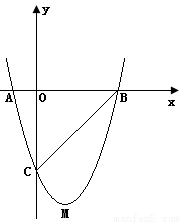

(1)求抛物线的解析式.
(2)过C、O两点作⊙H交x轴于另一点D,交直线BC于另一点E,已知F(1.5,-1.5)(F与H不重合).求: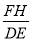 的值.
的值.
(3)若抛物线上有一点P,连PC交线段BM于Q点,且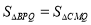 ,求P点的坐标.
,求P点的坐标.
(1)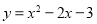 ;(2)
;(2)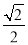 ;(3)(2,-3).
;(3)(2,-3).
【解析】
试题分析:(1)有抛物线求出C的坐标,由OC=OB,得到B的坐标,解关于m的一元二次方程即可得到m的值,从而得到抛物线的解析式;
(2)根据已知得到△OCB是等腰直角三角形,得出∠OBC=45°,由CD为⊙H的直径,得到△BED是直角三角形,从而得到△BED是等腰直角三角形,得到BD与ED的关系,根据作图得到,FH是△CBD的中位线,得到FH和BD的关系,从而得到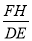 的值;
的值;
(3)首先确定出点C、M的坐标,再利用待定系数法求一次函数解析式求出直线BC的解析式,然后根据S△BPQ=S△CMQ时则S△BPC=S△BMC,利用等底同高的三角形的面积相等可知此时MP∥BC,然后根据互相平行的两直线的解析式的k值相等以及点M的坐标求出直线MP的解析式,联立抛物线解析式求解即可得到点P的坐标.
试题解析:(1)在 中,令
中,令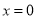 ,得:
,得: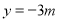 ,∴OC=
,∴OC=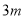 ,
,
∵OC=OB,∴ OB=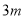 ,∴B(
,∴B(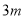 ,0),把B(
,0),把B(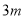 ,0)代入
,0)代入 中,得到:
中,得到: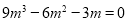 ,
,
∴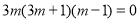 ,
,
∵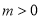 ,∴
,∴ ,∴
,∴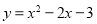 ;
;
(2)∵B(3,0),C(0,-3),F(1.5,-1.5),∴F为BC的中点,
∵H为CD的中点,∴FH为△CBD的中位线,∴FH=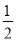 BD,
BD,
∵OC=OB,∴△OCB是等腰直角三角形,∴∠OBC=45°,∴∠EBD=45°,
∵CD为⊙H的直径,∴∠CED=90°,∴△BED是等腰直角三角形,∴BD=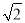 ED,
ED,
∴FH=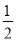 BD=
BD= ED,∴
ED,∴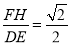 ;
;

(3)∵点C坐标为(0,﹣3),M(1,﹣4),
设直线BC的解析式为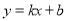 ,
,
则 ,解得:
,解得: ,
,
所以直线BC的解析式为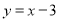 ,
,
∵S△BPQ=S△CMQ,∴S△BPQ+S△BCQ=S△CMQ+S△BCQ,即S△BPC=S△BMC,
∴点P到BC的距离等于点M到BC的距离,
∴MP∥BC,
设MP的解析式为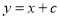 ,代入(1,-4)得:
,代入(1,-4)得:
则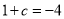 ,解得
,解得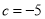 ,
,
所以,直线MP的解析式为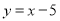 ,
,
联立 ,
,
解得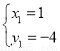 (为点M坐标),
(为点M坐标), ,
,
所以,点P的坐标为(2,﹣3).
考点:二次函数综合题.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
考点2:图形的相似
形状相同,大小不同的两个图形相似
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
考点2:图形的相似
形状相同,大小不同的两个图形相似
试题属性


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第一次摸底数学试卷(解析版) 题型:解答题
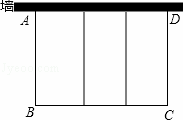
(8分)如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省平顶山市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
使用墙的一边,再用13m的铁丝网围成三边,围成一个面积为20m2的长方形,求这个长方形的两边长,设墙的对边长为x m,可得方程( )
A、x (13-x) =20 B、x·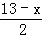 =20
=20
C、x (13- 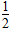 x ) =20 D、x·
x ) =20 D、x·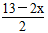 =20
=20
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南平顶山四十三中八年级上学期第一次段测数学试卷(解析版) 题型:填空题
直角三角形两直角边长分别为5cm,12cm,则斜边上的高为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南平顶山四十三中八年级上学期第一次段测数学试卷(解析版) 题型:选择题
若一个三角形的三边长的平方分别为:32,42,x2则此三角形是直角三角形的x2的值是()
A.42 B.52 C.7 D.52或7
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省武汉市武昌区部分学校九年级上学期期中联考数学试卷(解析版) 题型:解答题
(7分)已知,抛物线的顶点为P(3,—2),且在x轴上截得的线段AB=4.
(1)求抛物线的解析式.
(2)若点Q在抛物线上,且ΔQAB的面积为12,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省人教版九年级下学期模拟数学试卷(解析版) 题型:解答题
如图,在△ABC的外接圆O中,D是弧BC的中点,AD交BC于点E,连结BD.连结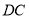 ,DC2=DE·DA是否成立?若成立,给出证明;若不成立,举例说明.
,DC2=DE·DA是否成立?若成立,给出证明;若不成立,举例说明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com