
【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.

(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?
【答案】(1)a=3;(2)铺设地面需要木地板757x;铺设地面需要地砖 7x+53;(3)小方家应选择B种活动方案,使铺设地面总费用(含材料费及安装费)更低.
【解析】
(1)根据长方形的对边相等可得a+5=4+4,即可求出a的值;
(2)根据三间卧室铺设木地板,其它区域铺设地砖,可知将三间卧室的面积的和为木地板的面积,用长方形的面积三间卧室的面积,所得的差为地砖的面积;
(3)根据卧室2的面积为21平方米求出x,再分别求出所需的费用,然后比较即可.
(1)根据题意,可得a+5=4+4,
解得a=3;
(2)铺设地面需要木地板:4×2x+a[10+6(2x1)x2x]+6×4
=8x+3(175x)+24=757x;
铺设地面需要地砖:16×8(757x)=12875+7x=7x+53;
(3)∵卧室2的面积为21平方米,
∴3[10+6(2x1)x2x]=21,
∴3(175x)=21,
∴x=2,
∴铺设地面需要木地板:757x=757×2=61,铺设地面需要地砖:7x+53=7×2+53=67.
A种活动方案所需的费用:61×300×0.8+67×100×0.85+2000=22335(元),
B种活动方案所需的费用:61×300×0.9+67×100×0.85=22165(元),
22335>22165,
所以小方家应选择B种活动方案,使铺设地面总费用(含材料费及安装费)更低.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
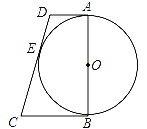
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=-![]() x+b的图象与反比例函数y2=
x+b的图象与反比例函数y2=![]() (x>0)的图象交于A、B两点,与x轴交于点C,且点A的坐标为(1,2),点B的横坐标为3.
(x>0)的图象交于A、B两点,与x轴交于点C,且点A的坐标为(1,2),点B的横坐标为3.
(1)在第一象限内,当x取何值时,y1>y2?(根据图直接写出结果)
(2)求反比例函数的解析式及△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() ,将其按分数段分为五组,绘制出以下不完整表格:
,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
(1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
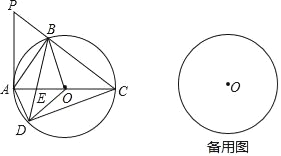
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
(1)求直线AB的表达式;
(2)求AC:CB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°.∠BOC=30°,OM平分∠AOC,ON平分∠BOC.

(1)求∠MON的度数;
(2)若∠BOC=60°,其他条件不变,则∠MON= ;
(3)若∠AOB=α,其他条件不变,求∠MON的度数;
(4)从上面的结果能看出什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com