
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.

【答案】(1)8-2t, ![]() .(2)不存在;当点Q的速度为每秒
.(2)不存在;当点Q的速度为每秒![]() 个单位长度时,经过
个单位长度时,经过![]() 秒,四边形PDBQ是菱形.(3)线段PQ中点M所经过的路径长为2
秒,四边形PDBQ是菱形.(3)线段PQ中点M所经过的路径长为2![]() 单位长度.
单位长度.
【解析】试题分析:(1)根据题意得:CQ=2t,PA=t,由Rt△ABC中,∠C=90°,AC=6,BC=8,PD∥BC,即可得tanA=![]() ,则可求得QB与PD的值;
,则可求得QB与PD的值;
(2)易得△APD∽△ACB,即可求得AD与BD的长,由BQ∥DP,可得当BQ=DP时,四边形PDBQ是平行四边形,即可求得此时DP与BD的长,由DP≠BD,可判定PDBQ不能为菱形;然后设点Q的速度为每秒v个单位长度,由要使四边形PDBQ为菱形,则PD=BD=BQ,列方程即可求得答案;
(3)设E是AC的中点,连接ME.当t=4时,点Q与点B重合,运动停止.设此时PQ的中点为F,连接EF,由△PMN∽△PQC.利用相似三角形的对应边成比例,即可求得答案.
试题解析:(1)根据题意得:CQ=2t,PA=t,
∴QB=8-2t,
∵在Rt△ABC中,∠C=90°,AC=6,BC=8,PD∥BC,
∴∠APD=90°,
∴tanA=![]() ,
,
∴PD= ![]() .
.
(2)不存在
在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=10
∵PD∥BC,
∴△APD∽△ACB,
∴![]() ,即
,即![]() ,
,
∴AD= ![]() ,
,
∴BD=AB-AD=10- ![]() ,
,
∵BQ∥DP,
∴当BQ=DP时,四边形PDBQ是平行四边形,
即8-2t= ![]() ,解得:t=
,解得:t=![]() .
.
当t=![]() 时,PD=
时,PD=![]() ,BD=10-
,BD=10-![]() ,
,
∴DP≠BD,
∴PDBQ不能为菱形.
设点Q的速度为每秒v个单位长度,
则BQ=8-vt,PD= ![]() ,BD=10-
,BD=10- ![]() ,
,
要使四边形PDBQ为菱形,则PD=BD=BQ,
当PD=BD时,即![]() =10-
=10- ![]() ,解得:t=
,解得:t=![]()
当PD=BQ,t=![]() 时,即
时,即![]() ,解得:v=
,解得:v=![]()
当点Q的速度为每秒![]() 个单位长度时,经过
个单位长度时,经过![]() 秒,四边形PDBQ是菱形.
秒,四边形PDBQ是菱形.
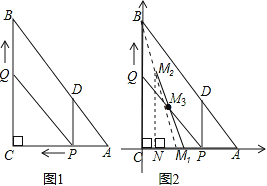
(3)如图2,以C为原点,以AC所在的直线为x轴,建立平面直角坐标系.
依题意,可知0≤t≤4,当t=0时,点M1的坐标为(3,0),当t=4时点M2的坐标为(1,4).
设直线M1M2的解析式为y=kx+b,
∴![]() ,
,
解得
![]() ,
,
∴直线M1M2的解析式为y=-2x+6.
∵点Q(0,2t),P(6-t,0)
∴在运动过程中,线段PQ中点M3的坐标(![]() ,t).
,t).
把x=![]() 代入y=-2x+6得y=-2×
代入y=-2x+6得y=-2×![]() +6=t,
+6=t,
∴点M3在直线M1M2上.
过点M2作M2N⊥x轴于点N,则M2N=4,M1N=2.
∴M1M2=2![]()
∴线段PQ中点M所经过的路径长为2![]() 单位长度.
单位长度.


科目:初中数学 来源: 题型:
【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.

(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,仅用直尺和圆规画一个长方形,使它的面积是图中长方形面积的4倍.
(2)若新的长方形的长与宽的比为4:3,且周长为56厘米,求新长方形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
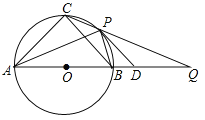
【题目】如图,等腰△ABC三个顶点在⊙O上,直径AB=12,P为弧BC上任意一点(不与B,C重合),直线CP交AB延长线与点Q,2∠PAB+∠PDA=90°,下列结论:①若∠PAB=30°,则弧BP的长为![]() ;②若PD//BC,则AP平分∠CAB;③若PB=BD,则
;②若PD//BC,则AP平分∠CAB;③若PB=BD,则![]() ,④无论点P在弧
,④无论点P在弧![]() 上的位置如何变化,CP·CQ为定值. 正确的是___________.
上的位置如何变化,CP·CQ为定值. 正确的是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.
《九章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几 何?
译文:假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:有几个人共同出钱买鸡?鸡的价钱是多少:”
设有x个人共同买鸡,鸡的价钱是y钱,根据题意可列方程组为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,中小学生每天在校体育活动时间不低于![]() .为此,某县就“你每天在校体育活动时间是多少”的问题,随机调查了辖区内300名初中学生.根据调查结果绘制成统计图如图所示,其中
.为此,某县就“你每天在校体育活动时间是多少”的问题,随机调查了辖区内300名初中学生.根据调查结果绘制成统计图如图所示,其中![]() 组为
组为![]() ,
,![]() 组为
组为![]() ,
,![]() 组为
组为![]() ,
,![]() 组为
组为![]() .
.

请根据上述信息解答下列问题:
(1)本次调查数据的中位数落在______组内,众数落在______组内;
(2)若该辖区约4000名初中生,请你估计其中达到国家规定体育活动时间的人数;
(3)若![]() 组取
组取![]() ,
,![]() 组取
组取![]() ,
,![]() 组取
组取![]() ,
,![]() 组取
组取![]() ,试计算这300名学生平均每天在校体育活动的时间.
,试计算这300名学生平均每天在校体育活动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com