
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,则大楼AB的高度为米.
,则大楼AB的高度为米.
【答案】6 ![]() +29
+29
【解析】解:延长AB交DC于H,作EG⊥AB于G,如图所示:
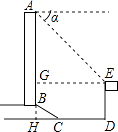
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1: ![]() ,
,
∴BH:CH=1: ![]() ,
,
设BH=x米,则CH= ![]() x米,
x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+( ![]() x)2=122,
x)2=122,
解得:x=6,∴BH=6米,CH=6 ![]() 米,
米,
∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=6 ![]() +20(米),
+20(米),
∵∠α=45°,
∴∠EAG=90°﹣45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6 ![]() +20(米),
+20(米),
∴AB=AG+BG=6 ![]() +20+9=(6
+20+9=(6 ![]() +29)m.
+29)m.
故答案为:6 ![]() +29.
+29.
根据题意添加辅助线,延长AB交DC于H,作EG⊥AB于G,由已知BC的长及BC的坡度=BH:CH,就可以求出BH、HC的长。即可求出BG、EG、DH的长,易证Rt△AEG是等腰直角三角形,就可求出AG的长,即可求得结果。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=CD=5厘米,AD=BC=4厘米. 动点P从A出发,以1厘米/秒的速度沿A→B运动,到B点停止运动;同时点Q从C点出发,以2厘米/秒的速度沿C→B→A运动,到A点停止运动.设P点运动的时间为t秒(t > 0),当t=____________时,S△ADP=S△BQD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,P是直线CD上的一个动点,(点P不与F重合)
(1)当点P在射线FC上移动时,∠FMP+∠FPM =∠AEF成立吗?请说明理由。
(2)当点P在射线FD上移动时,∠FMP+∠FPM与∠AEF有什么关系?并说明你的理由


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7 , …,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2017的横坐标为( )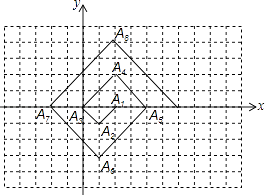
A.1010
B.2
C.1
D.﹣1006
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:![]() ;
;
(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2 , 且满足x12+x22=10,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( )
A.128°
B.126°
C.122°
D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com