
【题目】如图,在一个单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7 , …,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2017的横坐标为( )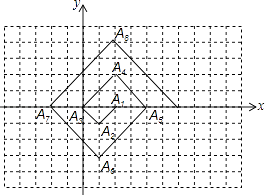
A.1010
B.2
C.1
D.﹣1006
【答案】A
【解析】解:∵A3是第一与第二个等腰直角三角形的公共点,
A5是第二与第三个等腰直角三角形的公共点,
A7是第三与第四个等腰直角三角形的公共点,
A9是第四与第五个等腰直角三角形的公共点,
…,
∵2017=1008×2+1,
∴A2017是第1008个与第1009个等腰直角三角形的公共点,
∴A2017在x轴正半轴,
∵OA5=4,OA9=6,OA13=8,
…,
∴OA2017=(2017+3)÷2=1010,
∴点A2017的坐标为(1010,0).
所以答案是:A.
【考点精析】掌握坐标确定位置是解答本题的根本,需要知道对于平面内任一点P,过P分别向x轴,y轴作垂线,垂足分别在x轴,y轴上,对应的数a,b分别叫点P的横坐标和纵坐标.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】计算题计算:(﹣2017)0+|1﹣ ![]() |﹣2cos45°+(﹣
|﹣2cos45°+(﹣ ![]() )﹣2;
)﹣2;
(1)计算:(﹣2017)0+|1﹣ ![]() |﹣2cos45°+(﹣
|﹣2cos45°+(﹣ ![]() )﹣2;
)﹣2;
(2)解不等式组:  .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,各地“广场舞”噪音干扰的问题备受关注,相关人员对本地区15﹣65岁年龄段的500名市民进行了随机调查,在调查过程中对“广场舞”噪音干扰的态度有以下五种:A:没影响;B:影响不大;C:有影响,建议做无声运动,D:影响很大,建议取缔;E:不关心这个问题,将调查结果绘统计整理并绘制成如下两幅不完整的统计图.
请根据以上信息解答下列问题:
(1)填空m= , 态度为C所对应的圆心角的度数为;
(2)补全条形统计图;
(3)若全区15﹣65岁年龄段有20万人,估计该地区对“广场舞”噪音干扰的态度为B的市民人数;
(4)若在这次调查的市民中,从态度为A的市民中抽取一人的年龄恰好在年龄段15﹣35岁的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知
内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知![]() ,图中阴影部分的面积之和为31,则矩形
,图中阴影部分的面积之和为31,则矩形![]() 的周长为___________.
的周长为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明拿两个大小不等直角三角板作拼图,如图①小三角板的斜边与大三角板直角边正好重合,已知:AD=1,∠B=∠ACD=30°.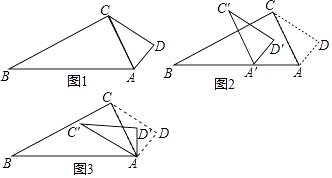
(1)AB的长;四边形ABCD的面积=(直接填空);
(2)如图2,若小明将小三角板ACD沿着射线AB方向平移,设平移的距离为m(平移距离指点A沿AB方向锁经过的线段长度),当点D平移到线段大三角板ABC的边上时,求出相应的m的值;
(3)如图3,小明将小三角板ACD绕点A顺时针旋转一个角α(0°<α<180°),记旋转中的△ACD为△AC′D′,在旋转过程中,设C′D′所在的直线与直线BC交于点P,与直线AB交于点Q,是否存在这样的P、Q两点,使△BPQ为等腰三角形?若存在,请直接求出此时D′Q的长;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,则大楼AB的高度为米.
,则大楼AB的高度为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)老张种植柑橘的成本是800元/吨,当客商采购量是多少时,老张在这次销售柑橘时获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com