
【题目】如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
根据题意可得CF=BF,∠F=90°,根据平行四边形与正方形的的判定即可判断①;根据菱形与正方形的判定即可判断②;根据矩形与正方形的判定即可判断③;根据正方形的判定即可判断.
∵四边形ABCD是矩形,
∴∠DCB=∠ABC=90°,
∵FB与FC分别平分∠ABC和∠BCD,
∴∠FCB=![]() ∠DCB=45°,∠FBC=
∠DCB=45°,∠FBC=![]() ∠ABC=45°,
∠ABC=45°,
∴∠FCB=∠FBC=45°,
∴CF=BF,∠F=180°﹣45°﹣45°=90°,
①∵EB∥CF,CE∥BF,
∴四边形BFCE是平行四边形,
∵CF=BF,∠F=90°,
∴四边形BFCE是正方形,故①正确;
∵BE=CE,BF=BE,CF=BF,
∴BF=CF=CE=BE,
∴四边形BFCE是菱形,
∵∠F=90°,
∴四边形BFCE是正方形,故②正确;
∵BE∥CF,CE⊥BE,
∴CF⊥CE,
∴∠FCE=∠E=∠F=90°,
∴四边形BFCE是矩形,
∵BF=CF,
∴四边形BFCE是正方形,故③正确;
∵CE∥BF,∠FBC=∠FCB=45°,
∴∠ECB=∠FBC=45°,∠EBC=∠FCB=45°,
∵∠F=90°,
∴∠FCE=∠FBE=∠F=90°,
∵BF=CF,
∴四边形BFCE是正方形,故④正确;
即正确的个数是4个.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在一个单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7 , …,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2017的横坐标为( )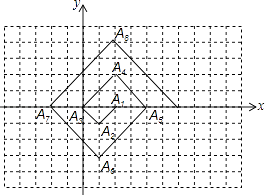
A.1010
B.2
C.1
D.﹣1006
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 ![]() 的值等于 .
的值等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从数﹣2,﹣ ![]() ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn,则正比例函数y=kx的图象经过第三、第一象限的概率是 .
,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn,则正比例函数y=kx的图象经过第三、第一象限的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注.某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请根据统计图中所提供的信息解答下列问题:
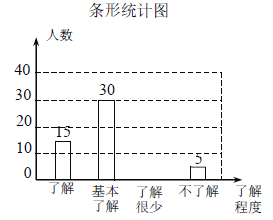
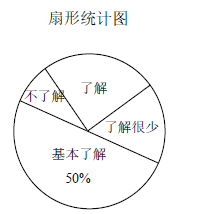
(1)接受问卷调查的学生共有 人;
(2)扇形统计图中“了解”部分所对应扇形的圆心角为 度;
(3)请补全条形统计图;
(4)若该中学共有学生1200人,则该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,E为CD边上一点,且AE、BE分别平分∠DAB、∠ABC.

(1)求证:△ADE≌△BCE;
(2)已知AD=3,求矩形的另一边AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P在∠AOB内,点M、N分别是点P关于AO、BO所在直线的对称点.
(1)若△PEF的周长为20,求MN的长.
(2)若∠O=50°,求∠EPF的度数.
(3)请直接写出∠EPF与∠O的数量关系是_____________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 是矩形,点
是矩形,点![]() 的坐标分别为
的坐标分别为![]() ,点
,点![]() 以
以![]() 的速度从
的速度从![]() 出发向终点
出发向终点![]() 运动,点
运动,点![]() 以
以![]() 的速度从
的速度从![]() 出发向终点
出发向终点![]() 运动,当
运动,当![]() 是以
是以![]() 为一腰的等腰三角形时,点
为一腰的等腰三角形时,点![]() 的坐标为____.
的坐标为____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com