
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 ![]() 的值等于 .
的值等于 . 
【答案】![]()
【解析】解:在正方形ABCD中,
∵∠ABD=∠CBD=45°,
∵四边形MNPQ和AEFG均为正方形,
∴∠BEF=∠AEF=90°,∠BMN=∠QMN=90°,
∴△BEF与△BMN是等腰直角三角形,
∴FE=BE=AE= ![]() AB,BM=MN=QM,
AB,BM=MN=QM,
同理DQ=MQ,
∴MN= ![]() BD=
BD= ![]() AB,
AB,
∴ ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】近年来,各地“广场舞”噪音干扰的问题备受关注,相关人员对本地区15﹣65岁年龄段的500名市民进行了随机调查,在调查过程中对“广场舞”噪音干扰的态度有以下五种:A:没影响;B:影响不大;C:有影响,建议做无声运动,D:影响很大,建议取缔;E:不关心这个问题,将调查结果绘统计整理并绘制成如下两幅不完整的统计图.
请根据以上信息解答下列问题:
(1)填空m= , 态度为C所对应的圆心角的度数为;
(2)补全条形统计图;
(3)若全区15﹣65岁年龄段有20万人,估计该地区对“广场舞”噪音干扰的态度为B的市民人数;
(4)若在这次调查的市民中,从态度为A的市民中抽取一人的年龄恰好在年龄段15﹣35岁的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)老张种植柑橘的成本是800元/吨,当客商采购量是多少时,老张在这次销售柑橘时获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
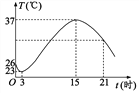
【题目】温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,点E是AB上的动点,点E与点A、B不重合,点D在CB的延长线上,且EC=ED.
(1)如图1,当BE=AE时,求证:BD=AE;
(2)当BE≠AE时,“BD=AE”能否成立?若不成立,请直接写出BD与AE数理关系,若成立,请给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线 AC、BD 相交成的锐角α=30°,若 AC=8,BD=6,则□ABCD的面积是( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=155°,第一步:在△ABC的上方确定点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB;第二步:在△A1BC的上方确定点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA;…,照此继续,最多能进行_____步.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com