
【题目】如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求F的坐标.

【答案】(1)(5,8);(2)向右平移5个单位,再向上平移3个单位;(3)F(![]() ,0).
,0).
【解析】
(1)根据点B移动到A的平移规律可得结论.
(2)根据点B移动到A的平移规律可得结论.
(3)作CH⊥OF于H.设F(m,0),根据S△AOF=S四边形AOHC+S△CHF,列出方程求出m的值.
解:(1)∵点B向右平移2个单位,再向上平移5个单位得到点A,
∴点C(3,3)向右平移2个单位,再向上平移5个单位得到点D(5,8).
故答案为(5,8).
(2)向右平移5个单位,再向上平移3个单位
(3)作CH⊥OF于H.设F(m,0).
∵S△AOF=S四边形AOHC+S△CHF,
∴![]() ×5×m=
×5×m=![]() ×(3+5)×3+
×(3+5)×3+![]() ×3×(m﹣3),
×3×(m﹣3),
解得:m=![]() ,∴F(
,∴F(![]() ,0),
,0),
(也可连接OC,再利用面积求)



 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E,P,连接OE,∠ADC=60°,AB=![]() BC=2,下列结论:①∠CAD=30°;②BD=2
BC=2,下列结论:①∠CAD=30°;②BD=2![]() ;③S四边形ABCD=ABAC;④OE=
;③S四边形ABCD=ABAC;④OE=![]() AD;⑤S△BOE=
AD;⑤S△BOE=![]() .其中正确的个数有( )个
.其中正确的个数有( )个
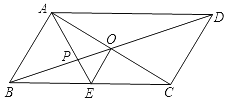
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
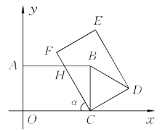
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7 , …,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2017的横坐标为( )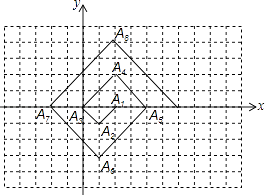
A.1010
B.2
C.1
D.﹣1006
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点在第一,四象限及x轴上运动,在第1次,它从原点运动到点(1,﹣1),用了1秒,然后按图中箭头所示方向运动,即(0,0)→(1,﹣1)→(2,0)→(3,1)→…,它每运动一次需要1秒,那么第2020秒时点所在的位置的坐标是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2 , 且满足x12+x22=10,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为![]() 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=
的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=![]() EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 ![]() 的值等于 .
的值等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,E为CD边上一点,且AE、BE分别平分∠DAB、∠ABC.

(1)求证:△ADE≌△BCE;
(2)已知AD=3,求矩形的另一边AB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com