Question

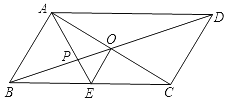
【题目】如图，平行四边形ABCD的对角线AC，BD相交于点O，AE平分∠BAD，分别交BC，BD于点E，P，连接OE，∠ADC＝60°，AB＝BC＝2，下列结论：①∠CAD＝30°；②BD＝2；③S四边形ABCD＝ABAC；④OE＝AD；⑤S△BOE＝．其中正确的个数有（ ）个

A.2B.3C.4D.5

Answer 1

【答案】D

【解析】

①先根据角平分线和平行线的性质得：∠BAE＝∠BEA，则AB＝BE＝2，由有一个角是60度的等腰三角形是等边三角形得：△ABE是等边三角形，由外角的性质和等腰三角形的性质得：∠ACE＝30°，最后由平行线的性质可作判断；

②先根据三角形中位线定理得：OE＝AB＝1，OE∥AB，根据勾股定理计算OC，OD的长，即可求BD的长；

③因为∠BAC＝90°，根据平行四边形的面积公式可作判断；

④根据三角形中位线定理可作判断；

⑤由三角形中线的性质可得：S△BOE＝S△EOC＝OEOC＝．

解：①∵AE平分∠BAD，

∴∠BAE＝∠DAE，

∵四边形ABCD是平行四边形，

∴AD∥BC，∠ABC＝∠ADC＝60°，

∴∠DAE＝∠BEA，

∴∠BAE＝∠BEA，

∴AB＝BE＝2，

∴△ABE是等边三角形，

∴AE＝BE＝2，

∵BC＝4，

∴EC＝2，

∴AE＝EC，

∴∠EAC＝∠ACE，

∵∠AEB＝∠EAC+∠ACE＝60°，

∴∠ACE＝30°，

∵AD∥BC，

∴∠CAD＝∠ACE＝30°，

故①正确；

②∵BE＝EC，OA＝OC，

∴OE＝AB＝1，OE∥AB，

∴∠EOC＝∠BAC＝60°+30°＝90°，

Rt△EOC中，OC＝，

∵四边形ABCD是平行四边形，

∴∠BCD＝∠BAD＝120°，

∴∠ACB＝30°，

∴∠ACD＝90°，

Rt△OCD中，OD＝

BD＝2OD＝2

故②正确

③由②知：∠BAC＝90°，

∴SABCD＝ABAC，

故③正确；

④由②知：OE是△ABC的中位线，

∴OE＝AB，

∵AB＝BC，

∴OE＝BC＝AD，

故④正确；

⑤∵BE＝EC＝2

∴S△BOE＝S△EOC＝OEOC＝

故⑤正确

故选：D．