
【题目】如图1,矩形ABCD中,P是AB边上的一点(不与A,B重合),PE平分∠APC交射线AD于E,过E作EM⊥PE交直线CP于M,交直线CD于N.
(1)求证:CM=CN;
(2)若AB:BC=4:3,
①当 ![]() =时,E恰好是AD的中点;
=时,E恰好是AD的中点;
②如图2,当△PEM与△PBC相似时,求 E N E M 的值. 
【答案】
(1)证明:延长PE交CD的延长线于F,如图1所示:
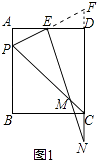
∵四边形ABCD是矩形,
∴AB∥CD,∠A=∠ADC=∠EDF═90°,AB=CD,AD=BC,
∴∠APE+∠AEP=90°,
∴∠F=∠APE,
∵EM⊥EN,
∴∠PEN=∠FEN=90°,
∴∠CPE+∠PME=90°,∠F+∠N=90°,
∵PE平分∠APC,
∴∠APE=∠MPE,
又∵∠PME=∠CMN,
∴∠CMN=∠N,
∴CM=CN
(2)["![]() ,解:分两种情况:①若△PEM∽△CCBP,则∠EPM=∠BCP,∴PE∥BC,不成立;②若△PEM∽△PBC,则∠APB=∠EPM=∠BPC=60°,设AB=4a,BC=AD=3a,则PB=
,解:分两种情况:①若△PEM∽△CCBP,则∠EPM=∠BCP,∴PE∥BC,不成立;②若△PEM∽△PBC,则∠APB=∠EPM=∠BPC=60°,设AB=4a,BC=AD=3a,则PB= ![]() a,AP=(4﹣
a,AP=(4﹣ ![]() )a,AE=(4
)a,AE=(4 ![]() ﹣3)a,设PE与CD交于点F,如图3所示:
﹣3)a,设PE与CD交于点F,如图3所示:![]() ∵AB∥CD,∴∠EFN=∠BFC=∠APE=60°,∴∠N=∠M=90°﹣60°=30°,∵EM⊥PE,∴∠NEF=∠PEM=90°,∴△PEM∽△FEN,∴
∵AB∥CD,∴∠EFN=∠BFC=∠APE=60°,∴∠N=∠M=90°﹣60°=30°,∵EM⊥PE,∴∠NEF=∠PEM=90°,∴△PEM∽△FEN,∴ ![]() ,∵AB∥CD,∴
,∵AB∥CD,∴ ![]() ,∴
,∴ ![]() =
= ![]() =
= ![]() 【解析】(2)解:①若E是AD的中点,则M、N、C三点重合,
【解析】(2)解:①若E是AD的中点,则M、N、C三点重合,
∵E为AD的中点,
∴AE=DE,
在△APE和△DFE中, 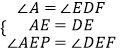 ,
,
∴△APE≌△DFE(ASA),
∴AP=DF,PE=FE,
∵EM⊥EN,
∴PC=FC,
∵FC=CD+DF,
∴AP+CD=PC,
设AD=3a,AB=4a,
过P作PF⊥CD于F,如图2所示:

设AP=DE=x,则PB=CF=4﹣x,PC=4+x,PF=3,
由勾股定理得:(4﹣x)2+32=(4+x)2,
解得:x= ![]() a,4﹣x=
a,4﹣x= ![]() a,
a,
∴ ![]() ;
;
【考点精析】通过灵活运用角的平分线判定和对顶角和邻补角,掌握可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点);两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个即可以解答此题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C(0,﹣3)
(1)请直接写出抛物线的解析式.
(2)抛物线的对称轴上是否存在一点P,使得△ACP的周长最短,若存在,请直接写出点P的坐标.
(3)点G的坐标是(2,﹣3),点F是x轴上一点,抛物线上是否存在点R,使得以A,G,F,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标.
(4)在B、C连线的下方抛物线上是否存在一点Q,使得△QBC的面积是△ABC的面积的一半?若存在,求出点Q的坐标.
(5)抛物线的顶点设为D,对称轴与y轴的交点为E,M(m,0)是x轴上一动点,点N是线段DE上的一点,若∠MNC=90°,请直接写出实数m的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据语句画图,并回答问题,如图,∠AOB内有一点P.
(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D.
(2)写出图中与∠CPD互补的角 .(写两个即可)
(3)写出图中∠O相等的角 .(写两个即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:![]() ;
;
(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E,P,连接OE,∠ADC=60°,AB=![]() BC=2,下列结论:①∠CAD=30°;②BD=2
BC=2,下列结论:①∠CAD=30°;②BD=2![]() ;③S四边形ABCD=ABAC;④OE=
;③S四边形ABCD=ABAC;④OE=![]() AD;⑤S△BOE=
AD;⑤S△BOE=![]() .其中正确的个数有( )个
.其中正确的个数有( )个
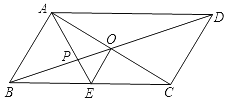
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
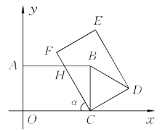
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com