
����Ŀ����֪��ͼ������y=ax2+bx+c��x�ύ�ڵ�A����1��0����B��3��0������y�ύ�ڵ�C��0����3��
��1����ֱ��д�������ߵĽ���ʽ��
��2�������ߵĶԳ������Ƿ����һ��P��ʹ�á�ACP���ܳ���̣������ڣ���ֱ��д����P�����꣮
��3����G�������ǣ�2����3������F��x����һ�㣬���������Ƿ���ڵ�R��ʹ����A��G��F��RΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����R�����꣮
��4����B��C���ߵ��·����������Ƿ����һ��Q��ʹ�á�QBC������ǡ�ABC�������һ�룿�����ڣ������Q�����꣮
��5�������ߵĶ�����ΪD���Գ�����y��Ľ���ΪE��M��m��0����x����һ���㣬��N���߶�DE�ϵ�һ�㣬����MNC=90�㣬��ֱ��д��ʵ��m�ı仯��Χ��
���𰸡�
��1���⣺��������y=ax2+bx+c��x�ύ�ڵ�A����1��0����B��3��0����
��y=a��x+1����x��3����
�ѵ�C��0����3������y=a��x+1����x��3���ã�a=1��
�������ߵĽ���ʽΪ��y=x2��2x��3
��2���⣺���ڣ���ͼ1
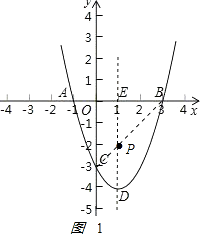 ��
��
����BC���Գ�����P��
��PA+PC=BC��̣�
����ACP���ܳ���̣�
��ֱ��BC�Ľ���ʽΪ��y=kx+b��
�� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��BC�Ľ���ʽΪ��y=x��3��
�������ߵĶԳ�����ֱ��x=1��
��x=1����y=x��3��
��y=��2��
��P��1����2��
��3���⣺���ڵ�R��ʹ����A��G��F��RΪ������ı�����ƽ���ı��Σ�
��ƽ���ı���ARGFʱ��RG��AF��yR=yG=��3��
��y=��3ʱ��x2��2x��3=��3�����x1=0��x2=2���ᣩ
��R1��0����3����
��ƽ���ı���AGFRʱ��yR+yG=0����yR=3����y=3ʱ��x2��2x��3=3�����x1=1�� ![]() ��x2=1+
��x2=1+ ![]() ��
��
R2��1�� ![]() ��3 ����R3��1+
��3 ����R3��1+ ![]() ��3����
��3����
�������������ڣ���R�����꣨0����3������1�� ![]() ��3 ������1+
��3 ������1+ ![]() ��3��
��3��
��4���⣺��ͼ2
 ��
��
��BC��ֱ��BC����ʽΪy=x��3����ABC��������6��
��ABC���QBCͬ�ף�
���BC�ϵĸ�ӦΪ ![]() ��
��
����C����CQ��BC����CQ= ![]() ���ٹ�Q��QH��y����H��
���ٹ�Q��QH��y����H��
��Rt��CHQ�ס�COB����Q��1����4������Q��ֱ��QL��BC��
ֱ��QL����ʽ�����y=x��5��
���������飬�� ![]() ��
��
��� ![]() ��
�� ![]() ��
��
������BC�����·����������ϴ������Q1��1����4��Q2��2����3��ʹ�á�QBC�ǡ�ABC�����һ��
��5���⣺��ͼ3
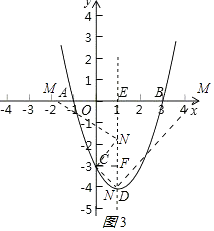 ��
��
������MNC=90�㣬����C��CF��DE�����CFN�ס�NEM����
![]() ��
��
��NE=n��M��m��0����D��1����4����C��0����3����
��CF=1��NE=n��FN=3��n��ME=1��m��
�������ʽ����
һԪ���η���n2��3n+��1��m��=0 ����n��һԪ���η����н⣬
��m�ݩ� ![]() ��
��
�ڵ���N�ƶ�����Dʱ����CNF�ǵ���ֱ�������Σ����ENM��Ȼ���ƣ�
����EM=EN=4��
���Դ�ʱm=5��
���Ͽ�֪ m�ķ�Χ�ǩ� ![]() ��m��5
��m��5
����������1�����ݴ���ϵ�������ɵô𰸣���2��������ԳƵ����ʣ��ɵ�A��B���ڶԳ���Գƣ������߶ε����ʿɵô𰸣���3������ƽ���ı��ε����ʿɵô𰸣���4����������ɵ�CQ�ij��ȣ�����ƽ���ߵ����ʣ��ɵ�QL�����ݽⷽ����ɵô𰸣���5���������������ε����ʣ��ɵù���n�ķ��̣����ݷ��̸����б�ʽ�ɵô𰸣��ٸ������������ε����ʿɵô𰸡�
�����㾫����������Ĺؼ���������ƽ���ߵ����ʵ����֪ʶ��������ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ������Լ���ƽ���ı��ε����ʵ����⣬�˽�ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣�


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
�У�![]() �ֱ���
�ֱ���![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ������ֱ���
������ֱ���![]() ��
��![]() �� �����������ۣ���
�� �����������ۣ���![]() ��
��![]() ��
��![]() ������ȷ���ǣ� ��
������ȷ���ǣ� ��

A.����B.�ڢ�C.�٢�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼEF��CD����1+��2��180�㣮
��1����˵��GD��CA��
��2����CDƽ�֡�ACB��DGƽ�֡�CDB���ҡ�A��40�㣬���ACB�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ACB�͡�ECD���ǵ���ֱ�������Σ���ACB����ECD��90�㣬DΪAB����һ�㣮
(1)��֤����ACE�ա�BCD��
(2)��AD��5��BD��12����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,AC=BC,��C=90��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AB������ΪE.��֤��AB=AC+CD.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ��һ�㣬�ֱ���
��һ�㣬�ֱ���![]() ��
��![]() Ϊ�ۺ۽������ǣ�
Ϊ�ۺ۽������ǣ�![]() ��
��![]() ���������𣬵�
���������𣬵�![]() ��
��![]() ǡ�ö�����
ǡ�ö�����![]() �ߵĵ�
�ߵĵ�![]() ������
������![]() ��
��![]() ����
����![]() ________��
________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� ![]() ABCD�У���DAB��60�㣬��E��F�ֱ���CD��AB���ӳ����ϣ���AE��AD��CF��CB��
ABCD�У���DAB��60�㣬��E��F�ֱ���CD��AB���ӳ����ϣ���AE��AD��CF��CB��

��1����֤���ı���AFCE��ƽ���ı��Σ�
��2����ȥ����֪�����ġ���DAB��60�㣬�����Ľ��ۻ������� ������������д��֤�����̣�������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD�У�P��AB���ϵ�һ�㣨����A��B�غϣ���PEƽ�֡�APC������AD��E����E��EM��PE��ֱ��CP��M����ֱ��CD��N��
��1����֤��CM=CN��
��2����AB��BC=4��3��
�ٵ� ![]() =ʱ��Eǡ����AD���е㣻
=ʱ��Eǡ����AD���е㣻
����ͼ2������PEM���PBC����ʱ���� E N E M ��ֵ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���������ε�������ƽ���߽���һ�㣬������Ϊ�����ε����ģ�����������Բ��Բ�ģ������ڹ涨������ı��ε��ĸ��ǵĽ�ƽ���߽���һ�㣬���ǰ������Ҳ��Ϊ���ı��ε����ġ���
��1���Ծٳ�һ�������ĵ��ı��Σ�
��2����ͼ1����֪��O���ı���ABCD�����ģ���֤��AB+CD=AD+BC��
��3����ͼ2��Rt��ABC�У���C=90�㣮O�ǡ�ABC�����ģ���ֱ��DE�ر�AC��BC�ڵ�D��E����O��Ȼ���ı���ABED�����ģ�������ֱ��DE�ɻ�������������ͼ2�л���һ������������ֱ��DE������˵��������
��4�����⣨3���У���AC=3��BC=4������������һ��ֱ��DE��AB����DE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com