Question

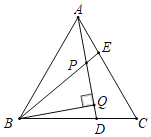
【题目】如图，△ABC为等边三角形，点D，E分别在BC，AC边上，且AE＝CD，

AD，BE相交于点P．

（1）求证：△ABE≌△CAD．

（2）求∠BPD的度数．

（3）若BQ⊥AD于Q，PQ＝3，PE＝1，求AD的长．

Answer 1

【答案】（1）证明见解析；（2）60°；（3）7.

【解析】

（1）由SAS证明△ABE≌△CAD即可；
（2）由三角形全等可以得出∠ABE=∠CAD，由外角与内角的关系就可以得出答案．
（3）由全等三角形的性质得出BE=AD，求出∠BPQ=30°，由直角三角形的性质求出BP的长，即可求得BE的长，即可解题．

（1）证明：∵△ABC为等边三角形，

∴AB＝BC＝AC，∠ABC＝∠ACB＝∠BAC＝60°．

在△ABE和△CAD中，，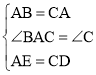

∴△ABE≌△CAD（SAS）；

（2）解：由（1）得：△ABE≌△CAD，

∴∠ABE＝∠CAD．

∵∠BAD+∠CAD＝60°，

∴∠BAD+∠ABE＝60°．

∴∠BPD＝∠ABE+∠BAD＝60°．

（3）解：∵△ABE≌△CAD，

∴BE＝AD，

∵BQ⊥AD，

∴∠PBQ＝90°﹣∠BPD＝30°，

∴BP＝2PQ＝6，

∴AD＝BE＝BP+PE＝6+1＝7．