
【题目】请在下面括号里补充完整证明过程:
已知:如图,△ABC中,∠ACB=90°,AF平分∠CAB,交CD于点E,交CB于点F,且∠CEF=∠CFE.求证:CD⊥AB.

证明:∵AF平分∠CAB (已知)
∴ ∠1=∠2( )
∵∠CEF=∠CFE , 又∠3=∠CEF (对顶角相等)
∴∠CFE=∠3(等量代换)
∵在△ACF中,∠ACF=90°(已知)
∴( )+∠CFE=90°( )
∵∠1=∠2, ∠CFE=∠3(已证) ∴( )+( )=90°(等量代换)
在△AED中, ∠ADE=90°( 三角形内角和定理)
∴ CD⊥AB( ).
【答案】角平分线的定义;∠CAF;直角三角形中两锐角互余;∠2;∠3;垂直的定义
【解析】
首先根据角平分线定义可得∠1=∠2,然后再利用等量代换可得∠CFE=∠3,根据直角三角形中两锐角互余,得到∠CAF+∠CFE=90°,进而可得∠2+∠3=90°,再根据三角形内角和定理得∠ADE=90°,进而得到CD⊥AB.
证明:∵AF平分∠CAB (已知)
∴ ∠1=∠2(角平分线的定义)
∵∠CEF=∠CFE , 又∠3=∠CEF (对顶角相等)
∴∠CFE=∠3(等量代换)
∵在△ACF中,∠ACF=90°(已知)
∴∠CAF+∠CFE=90°(直角三角形中两锐角互余)
∵∠1=∠2, ∠CFE=∠3(已证) ∴(∠2)+(∠3)=90°(等量代换)
在△AED中, ∠ADE=90°(三角形内角和定理)
∴ CD⊥AB(垂直的定义).
故答案为:角平分线的定义;∠CAF;直角三角形中两锐角互余;∠2;∠3;垂直的定义.


科目:初中数学 来源: 题型:
【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.
(1)求2015年至2017年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的情况,该地区到2019年需投入教育经费4250万元.如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
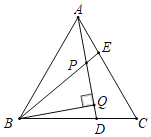
【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,
AD,BE相交于点P.
(1)求证:△ABE≌△CAD.
(2)求∠BPD的度数.
(3)若BQ⊥AD于Q,PQ=3,PE=1,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是( )

A.(2n﹣1,2n﹣1)B.(2n﹣1+1,2n﹣1)
C.(2n﹣1,2n﹣1)D.(2n﹣1,n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,点P是∠AOB内的定点且OP=![]() ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )

A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120 ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点。且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系。 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com