
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.

【答案】m<![]() .
.
【解析】
利用待定系数法解答,得出平移后得到的直线,求出A、B点的坐标,转化为直角三角形中的问题,再由直线与圆的位置关系的判定解答.
把点(12,﹣5)代入直线y=kx得,
﹣5=12k,
∴k=﹣![]() ;
;
由y=﹣![]() x平移m(m>0)个单位后得到的直线l所对应的函数关系式为y=﹣
x平移m(m>0)个单位后得到的直线l所对应的函数关系式为y=﹣![]() x+m(m>0),
x+m(m>0),
设直线l与x轴、y轴分别交于点A、B,(如图所示)
当x=0时,y=m;当y=0时,x=![]() m,
m,
∴A(![]() m,0),B(0,m),
m,0),B(0,m),
即OA=![]() m,OB=m,
m,OB=m,
在Rt△OAB中,AB=![]() m,
m,
过点O作OD⊥AB于D,
∵S△ABO=![]() ODAB=
ODAB=![]() OAOB,
OAOB,
∴![]() OD
OD![]() =
=![]() ×
×![]() ×
×![]() ,
,
∵m>0,解得OD=![]() m,
m,
由直线与圆的位置关系可知![]() m<6,解得m<
m<6,解得m<![]() ,
,
故答案为:m<![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(﹣5,0),且![]() ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,是否存在一点P,使△PAC是等腰三角形?若存在,请写出满足条件的所有P点的坐标并求t的值;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
(销售利润=销售价-成本价)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在下面括号里补充完整证明过程:
已知:如图,△ABC中,∠ACB=90°,AF平分∠CAB,交CD于点E,交CB于点F,且∠CEF=∠CFE.求证:CD⊥AB.

证明:∵AF平分∠CAB (已知)
∴ ∠1=∠2( )
∵∠CEF=∠CFE , 又∠3=∠CEF (对顶角相等)
∴∠CFE=∠3(等量代换)
∵在△ACF中,∠ACF=90°(已知)
∴( )+∠CFE=90°( )
∵∠1=∠2, ∠CFE=∠3(已证) ∴( )+( )=90°(等量代换)
在△AED中, ∠ADE=90°( 三角形内角和定理)
∴ CD⊥AB( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
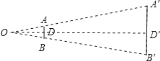
【题目】如图,数学趣闻:上世纪九十年代,国外有人传说:“从月亮上看地球,长城是肉眼唯一看得见的建筑物.”设长城的厚度为![]() ,人的正常视力能看清的最小物体所形成的视角为
,人的正常视力能看清的最小物体所形成的视角为![]() ,且已知月、地两球之间的距离为
,且已知月、地两球之间的距离为![]() ,根据学过的数学知识,你认为这个传说________.(请填“可能”或“不可能”,参考数据:
,根据学过的数学知识,你认为这个传说________.(请填“可能”或“不可能”,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如图所示的尚不完整的统计图表.
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 |

(1)在图①中,“7分”所在扇形的圆心角等于______![]() ;
;
(2)请你将②的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好;
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
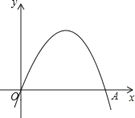
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个矩形的长为a,宽为b(a>0,b>0),则矩形的面积为ab.代数式xy(x>0,y>0)可以看作是边长为x和y的矩形的面积.我们可以由此解一元二次方程:x2+x﹣6=0(x>0).具体过程如下:
①方程变形为x(x+1)=6.
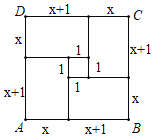
②画四个边长为x+1、x的矩形如图放置;
③由面积关系求解方程.
∵SABCD=(x+x+1)2,又SABCD=4x(x+1)+12.
∴(x+x+1)2=4x(x+1)+1,又x(x+1)=6,
∴(2x+1)2=25,
∵x>0,
∴x=2.
参照上述方法求关于x的二次方程x2+mx﹣n=0的解(x>0,m>0,n>0).(要求:画出示意图,标注相关线段的长度,写出解题步骤)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com