
【题目】如图,数学趣闻:上世纪九十年代,国外有人传说:“从月亮上看地球,长城是肉眼唯一看得见的建筑物.”设长城的厚度为![]() ,人的正常视力能看清的最小物体所形成的视角为
,人的正常视力能看清的最小物体所形成的视角为![]() ,且已知月、地两球之间的距离为
,且已知月、地两球之间的距离为![]() ,根据学过的数学知识,你认为这个传说________.(请填“可能”或“不可能”,参考数据:
,根据学过的数学知识,你认为这个传说________.(请填“可能”或“不可能”,参考数据:![]() )
)
【答案】不可能
【解析】
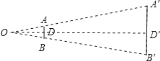
在直角三角形ODA中,AD=ODtan0.5′≈55.27m,即按照人的最小视角1′要想观察到地球上的长城,那么长城的厚度至少应该是2OD=110.54m,远远大于10,即以上所述是不可能的.
设∠AOB为正常视力观察长城所形成的夹角, 则AB=10m,∠AOB=1′,OD′⊥AB′.
在Rt△AOD中,tan∠AOD=![]() ,
,
∴OD=![]() ,
,
∵AD=![]() AB=5,∠AOD=
AB=5,∠AOD=![]() ∠AOB=0.5′.
∠AOB=0.5′.
∴OD=![]() ≈
≈![]() ≈34387.89(m)≈34.4(km).
≈34387.89(m)≈34.4(km).
这就是说,按照人的最小视角1′观察地球上长城的厚度,最远的距离只能是34.4km,而月球与地球之间的距离为380000km,这个数字很大,它相当于34.4km的11046倍,从这么远看长城,根本无法看见.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A在反比例函数y=![]() (x > 0)的图象上,作AB⊥y轴于B点.
(x > 0)的图象上,作AB⊥y轴于B点.
(1) △ABO的面积为 .
(2) 若点A的横坐标为4,点P在x轴的正半轴.且△OAP是等腰三角形,求点P的坐标: .
(3)动点M从原点出发,沿x轴的正方向运动,以MA为直角边,在MA的右侧作等腰Rt△MAN=90°,若在点M运动过程中,斜边MN始终在x轴上,求ON-OM的值
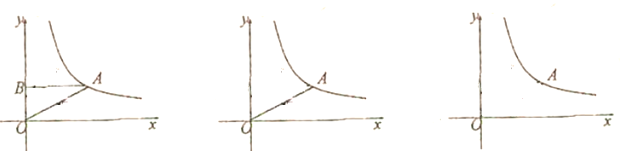
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=6, ∠BAC=30, ∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是___

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一个正比例函数图象y=2x和一个一次函数y=kx+b的图象交于点P(﹣2,a)且一次函数的图象与y轴的交点Q的纵坐标为4.
(1)求这两个函数的解析式;
(2)在同一坐标系中,分别画出这两个函数的图象;
(3)求△PQO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
(1)点A的坐标:_____;点B的坐标:_____;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作图:已知A(﹣2,1),B(﹣1,2),C(﹣3,4).
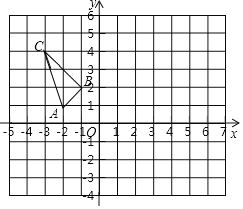
(1)画出与三角形ABC关于y轴对称的三角形A1B1C1;
(2)将三角形A1B1C1先向右平移2个单位,再向下平移1个单位,得到三角形A2B2C2,则三角形A2B2C2顶点坐标分别为:A2 B2 C2 ;
(3)若点P(a-1,b+2)与点A关于x轴对称,则a= ,b= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com