
����Ŀ��ij�������ۼס���������ë����֪������ë��ÿͲ���ۼ۱�������ë���15Ԫ������ʦ�Ӹ����깺����2Ͳ������ë���3Ͳ������ë������255Ԫ��
��1��������ס���������ë��ÿͲ���ۼ۸��Ƕ���Ԫ��
��2������������������������ò�����8780Ԫ�����ס���������ë��200Ͳ���Ҽ�����ë�����������������ë��������![]() ����֪������ë��ÿͲ�Ľ���Ϊ50Ԫ��������ë��ÿͲ�Ľ���Ϊ40Ԫ��
����֪������ë��ÿͲ�Ľ���Ϊ50Ԫ��������ë��ÿͲ�Ľ���Ϊ40Ԫ��
�����蹺��������ë��mͲ������������ļ��ֽ���������
������������ë�����ȫ���۳��������������������W��Ԫ���������ë�������m��Ͳ��֮��ĺ�����ϵʽ����˵����mΪ��ֵʱ�������������������Ƕ��٣�
���𰸡���1�������������ë��ÿͲ���ۼ�Ϊ60Ԫ��������ë��ÿͲ���ۼ�Ϊ45Ԫ����2���ٽ���������3�֣�������������ڵ�m=78ʱ��������������������Ϊ1390Ԫ��
����������1���������ë��ÿͲ���ۼ�ΪxԪ��������ë��ÿͲ���ۼ�ΪyԪ�����������з����飬�����ô𰸣�
��2�����蹺��������ë��mͲ����������ë��Ϊ��200��m��Ͳ���������ɵõ�����m�IJ���ʽ�飬������m��ȡֵ��Χ����mΪ������������m��ֵ��������ý���������
����m�ɱ�ʾ��W���ɵõ�����m��һ�κ���������һ�κ��������ʿ���ô𰸣�
��1���������ë��ÿͲ���ۼ�ΪxԪ��������ë��ÿͲ���ۼ�ΪyԪ��
��������ɵ�![]() �����
�����![]() ��
��
�𣺸����������ë��ÿͲ���ۼ�Ϊ60Ԫ��������ë��ÿͲ���ۼ�Ϊ45Ԫ��
��2����������������ë��mͲ����������ë��Ϊ��200��m��Ͳ��
��������ɵ� �����75��m��78��
�����75��m��78��
��m������
��m��ֵΪ76��77��78��
�����������3�֣��ֱ�Ϊ��
����һ������������ë��76Ͳ��������ë��Ϊ124Ͳ��
������������������ë��77Ͳ��������ë��Ϊ123Ͳ��
����һ������������ë��78Ͳ��������ë��Ϊ122Ͳ��
�ڸ�������ɵ�W=��60��50��m+��45��40����200��m��=5m+1000��
��5��0��
��W��m�������������75��m��78��
�൱m=78ʱ��W���W���ֵΪ1390��
�𣺵�m=78ʱ��������������������Ϊ1390Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
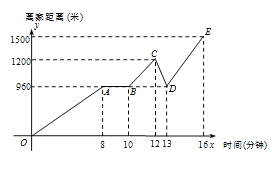
����Ŀ�����գ����������������ɫ��������ȫ�������ij��飬������ѧ���������г�ʱҪ���ؽ�ͨ����ע�⽻ͨ��ȫ����ĩ��С���ﹲ��������ͼ��ݣ�������һ��ʱ�����ijһ·�ڵȴ����̵ƣ����̵�����������ͼ��ݷ���ǰ����;��ͻȻ����Կ�ײ����ˣ������ż���ԭ·���أ��ڵȺ��̵Ƶ�·�ڴ��ҵ���Կ�ף������ǰ��ͼ��ݣ�С����Ҿ���������ʱ��Ĺ�ϵʾ��ͼ��ͼ��ʾ�������ͼ���ṩ����Ϣ�ش��������⣺
��1��ͼ���Ա������� ������������� ����
��2��С��ȴ����̵ƻ����� �����ӣ�
��3����ǰ��ͼ��ݵ�;�У�С��һ�������� ���ף�
��4��С������ ��ʱ��ε������ٶ���죬�����ٶ����� ����/�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ж��ģ����ش��������⣺���ǰ����Ƶĸ����ƹ㵽�ռ䣺��������������С��һ����ȣ�����״��ȫ��ͬ�����ǾͰ����ǽ��������壮
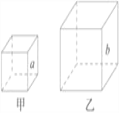
��ͼ���ס�����������ͬ�������壬�����嶼�������壬���ǵ�һ�ж�Ӧ�߶�֮�ȶ��������Ʊ�( a �� b )����S �� ��S �� �ֱ��ʾ������������ı��������![]()
������V �� ��V �� �ֱ��ʾ��������������������![]() ��
��
��1�����м������У�һ�����������������___��
A���������� B������Բ��
C������Բ���� D������������
��2������ɳ��������������Ҫ���ʣ����������һ�ж�Ӧ�߶�(��)�ıȵ���__________����������ı�����ıȵ���__________���������������ȵ���__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
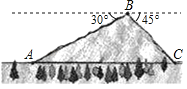
����Ŀ������304����ͨ�������ֹ��ն����������о���һ��ɽ�壬��ͼ��ʾ������ɽ��A��C���غ��θ߶�ԼΪ1000�ף�ɽ��B���ĺ��θ߶�ԼΪ1400�ף���B����ɽ��A���ĸ���Ϊ30������B����ɽ��C���ĸ���Ϊ45��������A��C���ؼ��ͨһ���������������Ϊ�����ף����ȡ�������ο�����![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
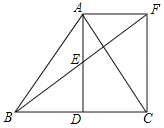
����Ŀ����ͼ����ABC�У�D��BC����һ�㣬E��AD���е㣬����A��BC��ƽ���߽�BE���ӳ�����F����AF=CD������CF��
��1����֤����AEF�ա�DEB��
��2����AB=AC�����ж��ı���ADCF����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ����O��BC���ϣ���BAC��ƽ���߽���O�ڵ�D������BD��CD������D��BC��ƽ������AC���ӳ����ཻ�ڵ�P��
��1����֤��PD�ǡ�O�����ߣ�
��2����֤����ABD�ס�DCP��
��3����AB=5cm��AC=12cmʱ�����߶�PC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[֪ʶ����]������������ѧ�г����Ļ���ͼ�Σ�����������֮��Ϊ180�㣮������������һ������������Σ����һ����������������ȣ���ô����������ǵ��������Σ���ȵ��������ԵĽ�Ҳ��ȣ�
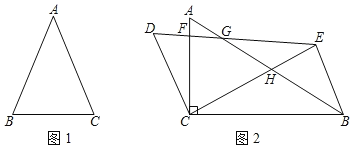
��ͼ1����������ABC�У����AB=AC����ô��B=��C��ͬ���������B=��C����AB=AC�������������Ҳ�ǵ��������Σ�
[֪ʶӦ��]����ͼ2����������ABC�У���ACB=90�㣬��ABC=30�㣬��������ABC�Ƶ�C��ʱ����ת��(0�㣼����60��)��(����ECB=����)���õ���Ӧ��������DEC��CE��AB�ڵ�H������BE����������BEHΪ���������Σ�����=____�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�У�ÿ���������б߳�Ϊ1 ��С��������ɣ�
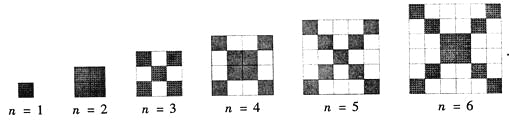
��1�� �۲�ͼ�Σ�����д���б���
�����α߳� | 1 | 3 | 5 | 7 | �� | n(����) |
��ɫС�����θ��� | �� | |||||
�����α߳� | 2 | 4 | 6 | 8 | �� | n(ż��) |
��ɫС�����θ��� | �� |
��2���ڱ߳�Ϊn��n��1�����������У����ɫС�����εĸ���ΪP1����ɫС�����εĸ���ΪP2�����Ƿ����ż��n��ʹP2��5P1�������ڣ���д��n��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ������![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() .��
.��![]() ���ӳ�����һ�㣬��
���ӳ�����һ�㣬��![]() ���߶���һ�㣬
���߶���һ�㣬![]() ����Ľ��ۣ� ��
����Ľ��ۣ� ��![]() ����
����![]() ����
����![]() �ǵȱ�������.
�ǵȱ�������.![]() ������ȷ���ǣ� ��
������ȷ���ǣ� ��
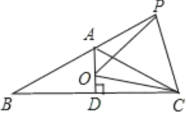
A. �٢ۢ�B. �٢ڢ�C. �٢�D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com