
【题目】近日,宝安区提出了“绿色环保,安全骑行”的倡议,号召中学生在骑自行车时要遵守交通规则,注意交通安全.周末,小峰骑共享单车到图书馆,他骑行一段时间后,在某一路口等待红绿灯,待绿灯亮起后继续向图书馆方向前进,途中突然发现钥匙不见了,于是着急地原路返回,在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家距离与所用时间的关系示意图如图所示.请根据图中提供的信息回答下列问题:
(1)图中自变量是 ,因变量是 ;
(2)小峰等待红绿灯花了 分钟;
(3)在前往图书馆的途中,小峰一共骑行 米;
(4)小峰在 时间段的骑行速度最快,最快的速度是 米/分.
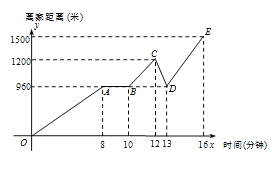
【答案】(1)x、y;(2)2;(3)1980;(4)12-13、240.
【解析】
(1)根据函数图象可以直接写出自变量和因变量;
(2)根据题意和函数图象可以得到小峰等待红绿灯所用的时间;
(3)根据函数图象可以得到小峰骑车走的总的路程;
(4)根据函数图象可以得到在哪个时间段内小峰的速度最快,并求出此时小峰的速度.
(1)由图可知,
图中自变量是x,因变量是y,
故答案为:x、y;
(2)由图可知,
小峰等待红绿灯花了:10-8=2(分钟),
故答案为:2;
(3)在前往图书馆的途中,小峰一共骑行了:1500+(1200-960)×2=1980米,
故答案为:1980;
(4)由图可知,
小峰在12-13时间段内速度最快,此时的速度为:(1200-960)÷1=240米/分,
故答案为:12-13、240.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
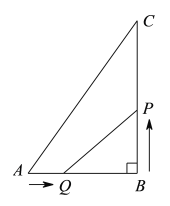
【题目】如图所示,已知在△ABC中,∠B=90°,AB=5 cm,BC=7 cm,点Q从点A开始沿AB边以1 cm/s的速度向点B移动,点P从点B开始沿BC边以2 cm/s的速度向点C移动,如果点Q,P分别从A,B两点同时出发,当一动点运动到终点,另一动点也随之停止运动.
(1)几秒后,△PBQ的面积等于4 cm2?
(2)几秒后,PQ的长度等于2![]() cm?
cm?
(3)在(1)中,△PBQ的面积能否等于7 cm2?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是( )
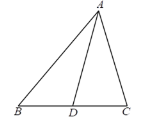
A. 2<AD<8B. 2<AD<4C. 1<AD<4D. 1<AD<8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
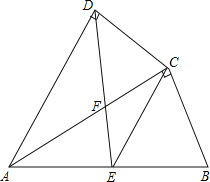
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=3 cm,BC=4 cm,动点P从点B出发以2 cm/s的速度向点C移动,动点Q从点C出发以1 cm/s的速度向点A移动,当一点到达终点时,另一点也随之停止运动.若动点P,Q同时出发,则经过多少秒时,PQ∥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB=BC=CD=AD=4cm,∠BAD=∠B=∠C=∠ADC=90°,点P以1cm/s的速度自点A向终点B运动,点Q同时以1cm/s的速度自点B向终点C运动,连接AQ、DP,设运动时间为t s.
(1)当t= s时,点P到达点B;
(2)求证:在运动过程中,△ABQ≌△DAP始终成立;
(3)如图2,作QM∥PD,且QM=PD,作MN⊥射线BC于点N,连接CM,请问在Q的运动过程中,∠MCN的度数是否改变?如果不变,请求出∠MCN;如果改变,请说明理由.
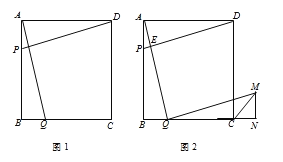
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人玩“石头、剪子、布”游戏,他们在不透明的袋子中放人形状、大小均相同的18张卡片,其中写有“石头”、“剪子”、“布”的卡片张数分别为5、6、7.两人先后各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“剪子”的概率是多少?
(2)若甲先摸出了“剪子”,则乙获胜的概率是多少?
(3)若甲先摸出了“布”,则甲获胜的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com