
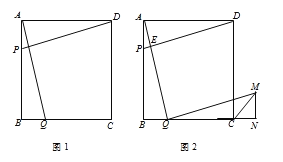
【题目】如图1,在四边形ABCD中,AB=BC=CD=AD=4cm,∠BAD=∠B=∠C=∠ADC=90°,点P以1cm/s的速度自点A向终点B运动,点Q同时以1cm/s的速度自点B向终点C运动,连接AQ、DP,设运动时间为t s.
(1)当t= s时,点P到达点B;
(2)求证:在运动过程中,△ABQ≌△DAP始终成立;
(3)如图2,作QM∥PD,且QM=PD,作MN⊥射线BC于点N,连接CM,请问在Q的运动过程中,∠MCN的度数是否改变?如果不变,请求出∠MCN;如果改变,请说明理由.
【答案】(1)4;(2)证明见解析;(3)∠MCN=45°.
【解析】
(1)根据AB=4cm,点P以1cm/s的速度自点A向终点B运动计算即可;
(2)根据题意得到AP=BQ,利用SAS定理证明;
(3)根据全等三角形的性质得到QM=AQ,∠AQB=∠QMN,证明△AQB≌△QMN,根据全等三角形的性质得到QN=AB,MN=BQ,结合图形证明即可.
(1)∵AB=4cm,点P以1cm/s的速度自点A向终点B运动,
∴点P到达点B所用的时间为:4÷1=4(s),
故答案为:4;
(2)在运动过程中,AP=BQ=t,
在△ABQ和△DAP中,
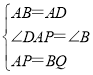 ,
,
∴△ABQ≌△DAP;
(3)∠MCN的度不改变,始终为45°,
理由如下:∵△ABQ≌△DAP,
∴AQ=DP,
∵QM=PD,
∴QM=AQ,
∵△ABQ≌△DAP,
∴∠BAQ=∠ADP,
∵∠BAQ+∠DAQ=90°,
∴∠ADP+∠DAQ=90°,即∠AED=90°,
∵QM∥PD,
∴∠AQM=∠AED=90°,
∴∠AQB+∠MQN=90°,
∴∠AQB=∠QMN,
在△AQB和△QMN中,
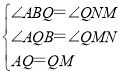 ,
,
∴△AQB≌△QMN,
∴QN=AB,MN=BQ,
∴BC=QN,
∴BC-QC=QN-QC,即BQ=CN,
∴MN=CN,
∴∠MCN=45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
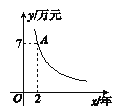
【题目】朱先生利用分期付款的形式购买了一套住房,他购买的住房的价格为24万元,交了首付之后每年付款y万元,x年结清余款,y与x的函数关系如图所示,请根据图象所提供的信息,回答下列问题:
(1)确定y与x的函数解析式,并求出首付款的数目;
(2)朱先生若用10年结清余款,则每年应付多少钱?
(3)如果朱先生打算每年付款不超过7000元,那么他至少需要几年才能结清余款?
查看答案和解析>>
科目:初中数学 来源: 题型:
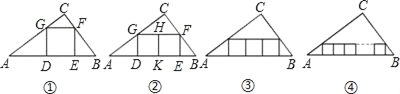
【题目】猜想归纳:为了建设经济型节约型社会,“先锋”材料厂把一批三角形废料重新利用,因此工人师傅需要把它们截成不同大小的正方形铁片.(已知:AC=40,BC=30,∠C=90°)
(1)如图①,若截取△ABC的内接正方形DEFG,请你求出此正方形的边长;
(2)如图②,若在△ABC内并排截取两个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(3)如图③,若在△ABC内并排截取三个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(4)猜想:如图④,假设在△ABC内并排截取n个相同的正方形,使它们组成的矩形内接于△ABC,则此正方形的边长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
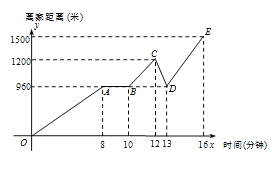
【题目】近日,宝安区提出了“绿色环保,安全骑行”的倡议,号召中学生在骑自行车时要遵守交通规则,注意交通安全.周末,小峰骑共享单车到图书馆,他骑行一段时间后,在某一路口等待红绿灯,待绿灯亮起后继续向图书馆方向前进,途中突然发现钥匙不见了,于是着急地原路返回,在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家距离与所用时间的关系示意图如图所示.请根据图中提供的信息回答下列问题:
(1)图中自变量是 ,因变量是 ;
(2)小峰等待红绿灯花了 分钟;
(3)在前往图书馆的途中,小峰一共骑行 米;
(4)小峰在 时间段的骑行速度最快,最快的速度是 米/分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B、C三点表示的数分别为a、b、c,其中AC=2BC,a、b满足|a+6|+(b﹣12)2=0.
![]()
(1)则a= ,b= ,c= .
(2)动点P从A点出发,以每秒2个单位的速度沿数轴向右运动,到达B点后立即以每秒3个单位的速度沿数轴返回到A点,设动点P的运动时间为t秒.
①P点从A点向B点运动过程中表示的数 (用含t的代数式表示).
②求t为何值时,点P到A、B、C三点的距离之和为18个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是![]()
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是![]()
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=![]() ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )

A. ![]() B. 3 C. 2 D. 2
B. 3 C. 2 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com