
【题目】猜想归纳:为了建设经济型节约型社会,“先锋”材料厂把一批三角形废料重新利用,因此工人师傅需要把它们截成不同大小的正方形铁片.(已知:AC=40,BC=30,∠C=90°)
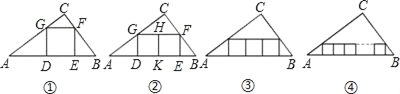
(1)如图①,若截取△ABC的内接正方形DEFG,请你求出此正方形的边长;
(2)如图②,若在△ABC内并排截取两个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(3)如图③,若在△ABC内并排截取三个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(4)猜想:如图④,假设在△ABC内并排截取n个相同的正方形,使它们组成的矩形内接于△ABC,则此正方形的边长是多少?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】
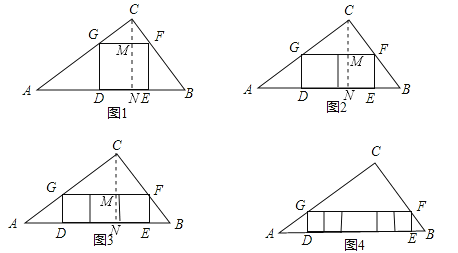
(1)根据题意画出图形,作CN⊥AB,再根据GF∥AB,可知△CGF∽△CAB,由平行得到两对同位角相等,进而得到两三角形相似,设出正方形的边长为x,根据相似三角形的性质得到比例式,进而列出关于x的方程,求出方程的解,即可求出正方形的边长;
(2)作CN⊥AB,交GF于点M,交AB于点N,同(1)可知,△CGF∽△CAB,根据对应边的比等于相似比,同理可求出正方形的边长;
(3)作CN⊥AB,交GF于点M,交AB于点N,同(1)可知,△CGF∽△CAB,根据对应边的比等于相似比,同理可求出正方形的边长;
(4)同理可得正方形的边长.
(1)在图1中作△ABC的高CN交GF于M.在Rt△ABC中,∵AC=40,BC=30,∴AB=50,CN=![]() =24.
=24.
由GF∥AB,得:△CGF∽△CAB,∴![]() .
.
设正方形的边长为x,则![]() ,解得:
,解得:![]() .
.
即正方形的边长为![]() .
.
(2)方法同(1),如图2.
△CGF∽△CAB,则![]() .
.
设小正方形的边长为x,则![]() ,解得:
,解得:![]() .
.
即小正方形的边长为![]() .
.
(3)在图3中,作CN⊥AB,交GF于点M,交AB于点N.
∵GF∥AB,∴△CGF∽△CAB,∴![]() =
=![]() ,设每个正方形的边长为x,则
,设每个正方形的边长为x,则![]() =
=![]() ,∴x=
,∴x=![]() ;
;
(4)设每个正方形的边长为x,同理得到:
则![]() =
=![]() ,则x=
,则x=![]() ,∴每个小正方形的边长为
,∴每个小正方形的边长为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
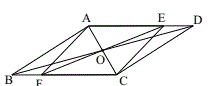
【题目】如图,在平行四边形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,并且
,并且![]() ,点
,点![]() 是
是![]() 边上一动点,延长
边上一动点,延长![]() 交于
交于![]() 点
点![]() ,当点
,当点![]() 从点
从点![]() 向点
向点![]() 移动过程中(点
移动过程中(点![]() 与点
与点![]() ,
,![]() 不重合),则四边形
不重合),则四边形![]() 的变化是( )
的变化是( )
A. 平行四边形→菱形→平行四边形→矩形→平行四边形
B. 平行四边形→矩形→平行四边形→菱形→平行四边形
C. 平行四边形→矩形→平行四边形→正方形→平行四边形
D. 平行四边形→矩形→菱形→正方形→平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连接NE、NM,过点N作NG平分∠ENM,交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF=__度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
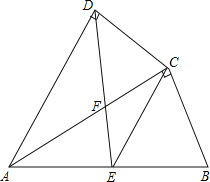
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有红、黑两种颜色的球共60只,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,七(4)班的数学学习小组做了摸球实验.他们]将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到下表中的一组统计数据:
摸球的次数n | 50 | 100 | 300 | 500 | 800 | 1000 | 2000 |
摸到红球的次数m | 14 | 33 | 95 | 155 | 241 | 298 | 602 |
摸到红球的频率 | 0.28 | 0.33 | 0.317 | 0.31 | 0.301 | 0.298 | 0.301 |
(1)请估计:当次数n足够大时,摸到红球的频率将会接近 ;(精确到0.1)
(2)假如你去摸一次,则摸到红球的概率的估计值为 ;
(3)试估算盒子里红球的数量为 个,黑球的数量为 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB=BC=CD=AD=4cm,∠BAD=∠B=∠C=∠ADC=90°,点P以1cm/s的速度自点A向终点B运动,点Q同时以1cm/s的速度自点B向终点C运动,连接AQ、DP,设运动时间为t s.
(1)当t= s时,点P到达点B;
(2)求证:在运动过程中,△ABQ≌△DAP始终成立;
(3)如图2,作QM∥PD,且QM=PD,作MN⊥射线BC于点N,连接CM,请问在Q的运动过程中,∠MCN的度数是否改变?如果不变,请求出∠MCN;如果改变,请说明理由.
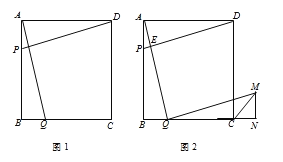
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校召集留守儿童过端午节,桌上摆有甲、乙两盘粽子,每盘中盛有白粽2个,豆沙粽1个,肉粽1个(粽子外观完全一样).
(1)小明从甲盘中任取一个粽子,取到豆沙粽的概率是 ;
(2)小明在甲盘和乙盘中先后各取了一个粽子,请用树状图或列表法求小明恰好取到两个白粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,一艘轮船以15海里/时的速度,由南向北航行,在A出测得小岛P在北偏西![]() 方向上,两小时后,轮船在B处测得小岛P在北偏西30°方向上.在小岛周围18海里内有暗礁,若轮船
方向上,两小时后,轮船在B处测得小岛P在北偏西30°方向上.在小岛周围18海里内有暗礁,若轮船
不改变方向仍继续向前航行,问:有无触礁的危险?说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com