
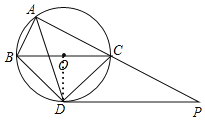
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.

【答案】(1)证明见解析;(2)证明见解析;(3)CP=16.9cm.
【解析】(1)先判断出∠BAC=2∠BAD,进而判断出∠BOD=∠BAC=90°,得出PD⊥OD即可得出结论;
(2)先判断出∠ADB=∠P,再判断出∠DCP=∠ABD,即可得出结论;
(3)先求出BC,再判断出BD=CD,利用勾股定理求出BC=BD=![]() ,最后用△ABD∽△DCP得出比例式求解即可得出结论.
,最后用△ABD∽△DCP得出比例式求解即可得出结论.
(1)如图,连接OD,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵AD平分∠BAC,
∴∠BAC=2∠BAD,
∵∠BOD=2∠BAD,
∴∠BOD=∠BAC=90°,
∵DP∥BC,
∴∠ODP=∠BOD=90°,
∴PD⊥OD,
∵OD是⊙O半径,
∴PD是⊙O的切线;
(2)∵PD∥BC,
∴∠ACB=∠P,
∵∠ACB=∠ADB,
∴∠ADB=∠P,
∵∠ABD+∠ACD=180°,∠ACD+∠DCP=180°,
∴∠DCP=∠ABD,
∴△ABD∽△DCP;
(3)∵BC是⊙O的直径,
∴∠BDC=∠BAC=90°,
在Rt△ABC中,BC=![]() =13cm,
=13cm,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠BOD=∠COD,
∴BD=CD,
在Rt△BCD中,BD2+CD2=BC2,
∴BD=CD=![]() BC=
BC=![]() ,
,
∵△ABD∽△DCP,
∴![]() ,
,
∴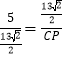 ,
,
∴CP=16.9cm.


科目:初中数学 来源: 题型:
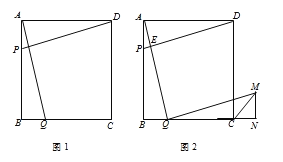
【题目】如图1,在四边形ABCD中,AB=BC=CD=AD=4cm,∠BAD=∠B=∠C=∠ADC=90°,点P以1cm/s的速度自点A向终点B运动,点Q同时以1cm/s的速度自点B向终点C运动,连接AQ、DP,设运动时间为t s.
(1)当t= s时,点P到达点B;
(2)求证:在运动过程中,△ABQ≌△DAP始终成立;
(3)如图2,作QM∥PD,且QM=PD,作MN⊥射线BC于点N,连接CM,请问在Q的运动过程中,∠MCN的度数是否改变?如果不变,请求出∠MCN;如果改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,一艘轮船以15海里/时的速度,由南向北航行,在A出测得小岛P在北偏西![]() 方向上,两小时后,轮船在B处测得小岛P在北偏西30°方向上.在小岛周围18海里内有暗礁,若轮船
方向上,两小时后,轮船在B处测得小岛P在北偏西30°方向上.在小岛周围18海里内有暗礁,若轮船
不改变方向仍继续向前航行,问:有无触礁的危险?说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市民打车出行常用交通工具为出租车和滴滴快车.该市两种车的收费标准如下:
出租车:2千米以内9元;超过2千米的部分:2元/千米.
滴滴快车:里程费:1.6元/千米;时长费:18元/小时;远途费:0.8元/千米.(注:滴滴快车的收费由里程费、时长费、远途费三部分组成,其中里程费按行车的实际里程计算;时长费按照行车的实际时间计算;远途费的收取方式为:行车不超过8千米,不收远途费,超过8千米的,超过部分每千米加收0.8元).假设打车的平均速度为30千米/小时.
(1)小明家到学校4千米,乘坐出租车需要多少元?
(2)设乘车路程为x(x>2)千米,分别写出出租车和滴滴快车的应收费用(用含x的代数式表示);
(3)小方和爸爸从家去环球中心(家到环球中心的距离天于2千米),乘坐滴滴快车比乘坐出租车节约2.4元,求小方家到环球中心的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
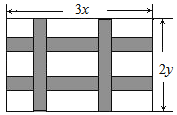
【题目】如图,要设计一幅长为3xcm,宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度为acm,竖彩条的宽度为bcm,问空白区域的面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com