
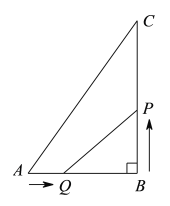
【题目】如图所示,已知在△ABC中,∠B=90°,AB=5 cm,BC=7 cm,点Q从点A开始沿AB边以1 cm/s的速度向点B移动,点P从点B开始沿BC边以2 cm/s的速度向点C移动,如果点Q,P分别从A,B两点同时出发,当一动点运动到终点,另一动点也随之停止运动.
(1)几秒后,△PBQ的面积等于4 cm2?
(2)几秒后,PQ的长度等于2![]() cm?
cm?
(3)在(1)中,△PBQ的面积能否等于7 cm2?试说明理由.
【答案】(1)1 s;(2)3 s;(3)△PBQ的面积不可能等于7 cm2.
【解析】
(1)设点P、Q的运动时间为x秒,则由题意可得:BQ=AB-AQ=5-x,BP=2x,根据三角形面积公式结合题中已知条件列出方程,解方程即可求得对应的运动时间;
(2)在Rt△PBQ中,由勾股定理可得BQ2+PB2=PQ2结合已知条件列出方程,解方程即可求得点P、Q对应的运动时间;
(3)同(1)列出关于点P、Q的运动时间x的方程,再根据根的判别式判断所列方程有无实数根即可得出结论.
(1)设x s后,△PBQ的面积等于4 cm2.
此时,AQ=x cm,QB=(5-x)cm,BP=2x cm.
由![]() BP·QB=4,得
BP·QB=4,得![]() ×2x(5-x)=4,
×2x(5-x)=4,
即x2-5x+4=0,
解得x1=1,x2=4(不合题意,舍去).
所以1 s后,△PBQ的面积等于4 cm2.
(2)在Rt△PBQ中,因为PQ=2![]() cm,根据勾股定理,得(5-x)2+(2x)2=(2
cm,根据勾股定理,得(5-x)2+(2x)2=(2![]() )2,
)2,
解得x1=3,x2=-1(舍去).
所以3 s后,PQ的长度等于2![]() cm.
cm.
(3)由(1),得![]() ×2x(5-x)=7.
×2x(5-x)=7.
整理,得x2-5x+7=0.
因为b2-4ac=25-28<0,
所以此方程无解.
所以△PBQ的面积不可能等于7 cm2.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
(1)求证:FG=FB.
(2)若tan∠F=![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
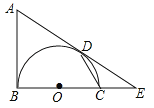
【题目】(2016浙江省丽水市)如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=27°,OB=2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个面积为150 m2的矩形养鸡场,为了节约材料,养鸡场的一边沿用原来的一堵墙,墙长为a m,其余三边用竹篱笆围成,已知竹篱笆的长为35 m.
(1)如果a=40,那么养鸡场的长和宽各为多少米?
(2)如果a是一个可以变化的量,那么墙的长度a对所建的养鸡场有怎样的影响?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)由大小相同的小立方块搭成的几何体如图1,请在图2的方格中画出该几何体的俯视图和左视图.
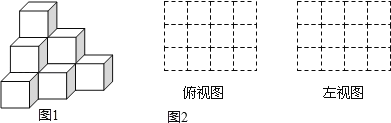
(2)用小立方体搭一个几何体,使得它的俯视图和左视图与你在方格中所画的一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
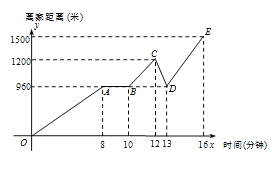
【题目】近日,宝安区提出了“绿色环保,安全骑行”的倡议,号召中学生在骑自行车时要遵守交通规则,注意交通安全.周末,小峰骑共享单车到图书馆,他骑行一段时间后,在某一路口等待红绿灯,待绿灯亮起后继续向图书馆方向前进,途中突然发现钥匙不见了,于是着急地原路返回,在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家距离与所用时间的关系示意图如图所示.请根据图中提供的信息回答下列问题:
(1)图中自变量是 ,因变量是 ;
(2)小峰等待红绿灯花了 分钟;
(3)在前往图书馆的途中,小峰一共骑行 米;
(4)小峰在 时间段的骑行速度最快,最快的速度是 米/分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com