
【题目】如图,在△ABC中,∠C=90°,AC=3 cm,BC=4 cm,动点P从点B出发以2 cm/s的速度向点C移动,动点Q从点C出发以1 cm/s的速度向点A移动,当一点到达终点时,另一点也随之停止运动.若动点P,Q同时出发,则经过多少秒时,PQ∥AB.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,要建一个面积为150 m2的矩形养鸡场,为了节约材料,养鸡场的一边沿用原来的一堵墙,墙长为a m,其余三边用竹篱笆围成,已知竹篱笆的长为35 m.
(1)如果a=40,那么养鸡场的长和宽各为多少米?
(2)如果a是一个可以变化的量,那么墙的长度a对所建的养鸡场有怎样的影响?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A的坐标为(m,0),点B的坐标为(0,n),其中m=![]() ,
,![]() =0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.
=0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.
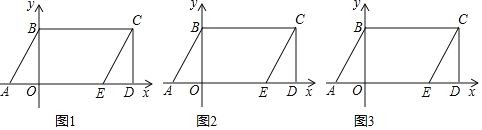
(1)如图1,分别求点C、点E的坐标;
(2)点P自点C出发,以每秒1个单位长度沿线段CB运动,同时点Q自点O出发,以每秒2个单位长度沿线段OE运动,连接AP、BQ,点Q运动至点E时,点P同时停止运动.设运动时间t(秒),三角形ABQ的面积与三角形APB的面积的和为s(平方单位),求s与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,BP:QE=8:3,此时将线段PQ向左平移2个单位长度得到线段P'Q'(点P'与点P对应),线段P′Q'再向下平移2个单位长度得到线段MN(点M与点P'对应),线段MN交x轴于点G,点H在线段OA上,OH=![]() OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.
OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )
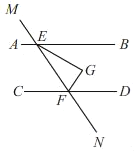
A. 20°B. 25°C. 35°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
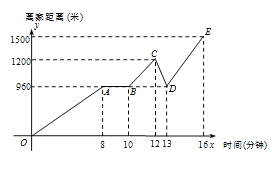
【题目】近日,宝安区提出了“绿色环保,安全骑行”的倡议,号召中学生在骑自行车时要遵守交通规则,注意交通安全.周末,小峰骑共享单车到图书馆,他骑行一段时间后,在某一路口等待红绿灯,待绿灯亮起后继续向图书馆方向前进,途中突然发现钥匙不见了,于是着急地原路返回,在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家距离与所用时间的关系示意图如图所示.请根据图中提供的信息回答下列问题:
(1)图中自变量是 ,因变量是 ;
(2)小峰等待红绿灯花了 分钟;
(3)在前往图书馆的途中,小峰一共骑行 米;
(4)小峰在 时间段的骑行速度最快,最快的速度是 米/分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选择适当的方法解下列方程:
(1)3(x+1)2=27; (2)2x2+6=7x;
(3)3x(x-2)=2(2-x); (4)y2-4y-3=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
如果小王和小张按上述规则各转动转盘一次,则
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
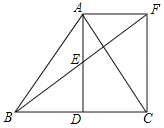
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com