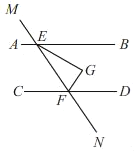
【题目】如图，AB∥CD，直线MN与AB、CD分别交于点E、F，FG平分∠EFD，EG⊥FG于点G，若∠CFN＝110°，则∠BEG＝（ ）
A. 20°B. 25°C. 35°D. 40°
【答案】C
【解析】
已知∠CFN＝110°，根据对顶角相等可得∠DFE＝∠CFN＝110°，因为FG平分∠EFD，由角平分线的定义可得∠EFG＝
∠EFD＝55°；再由EG⊥FG，可得∠G＝90°，即可求得∠GEF＝35°；又因AB∥CD,∠EFD＝110°，根据平行线的性质可得∠BEF＝70°，即可得∠BEG＝∠BEF﹣∠GEF＝35°.
∵∠CFN＝110°，
∴∠DFE＝∠CFN＝110°，
∵FG平分∠EFD，
∴∠EFG＝∠EFD＝55°，
又EG⊥FG，即∠G＝90°，
∴∠GEF＝35°，
∵AB∥CD,∠EFD＝110°，
∴∠BEF＝70°，
∴∠BEG＝∠BEF﹣∠GEF＝35°.
故选C.
科目：初中数学 来源： 题型：
【题目】如图，已知数轴上点A表示的数为6，点B是数轴上在A左侧的一点，且A，B两点间的距离为11，动点P从点A出发，以每秒3个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．
（1）数轴上点B表示的数是 ，当点P运动到AB中点时，它所表示的数是 ；
（2）动点Q从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，若P，Q两点同时出发，求点P与Q运动多少秒时重合？
（3）动点Q从点B出发，以每秒2个单拉长度的速度沿数轴向左匀速运动，若P，Q两点同时出发，求：
①当点P运动多少秒时，点P追上点Q？
②当点P与点Q之间的距离为8个单位长度时，求此时点P在数轴上所表示的数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按图中所标注的数据，计算图中实线所围成的面积S是（ ）
A.50B.62C.65D.68
查看答案和解析>>
科目：初中数学 来源： 题型：
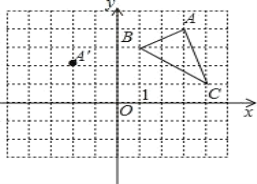
【题目】在平面直角坐标系中，△ABC 的三个顶点的位置如图所示，点 A′的坐标是(-2，2)，现将△ABC 平移，使点 A 变换为点 A′，点 B′、C′分别是 B、C 的对应点．
(1) 请画出平移后的△A′B′C′(不写画法)，并直接写出点B′、C′的坐标：B′ 、C′ ；
(2) 若△ABC 内部一点 P 的坐标为(
，
)，则点 P 的对应点 P′的坐标是 ；
(3) 连接 A′B，CC′，并求四边形 A′BCC′的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C＝90°，AC＝3 cm，BC＝4 cm，动点P从点B出发以2 cm/s的速度向点C移动，动点Q从点C出发以1 cm/s的速度向点A移动，当一点到达终点时，另一点也随之停止运动．若动点P，Q同时出发，则经过多少秒时，PQ∥AB.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（阅读材料）解方程(x－1)2－5(x－1)＋4＝0时，我们发现：先将x－1看作一个整体，然后设x－1＝y.……①，那么原方程可化为y2－5y＋4＝0，解得y1＝1，y2＝4.当y＝1时，x－1＝1，则x＝2；当y＝4时，x－1＝4，则x＝5，故原方程的解为x1＝2，x2＝5.
上述解题过程，在由原方程得到方程①的过程中，运用了“换元法”达到了解方程的目的，体现了转化的数学思想．
（解决问题）
(1)请利用以上知识解方程：(3x＋5)2－4(3x＋5)＋3＝0；
(2)在△ABC中，∠C＝90°，两条直角边的长分别为a，b，斜边的长为c，且(a2＋b2)(a2＋b2＋1)＝12，求斜边c的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
