
����Ŀ�����Ķ����ϣ��ⷽ��(x��1)2��5(x��1)��4��0ʱ�����Ƿ��֣��Ƚ�x��1����һ��������Ȼ����x��1��y.����������ôԭ���̿ɻ�Ϊy2��5y��4��0�����y1��1��y2��4.��y��1ʱ��x��1��1����x��2����y��4ʱ��x��1��4����x��5����ԭ���̵Ľ�Ϊx1��2��x2��5.
�����������������ԭ���̵õ����̢ٵĹ�����������������Ԫ�����ﵽ�˽ⷽ�̵�Ŀ����������ת������ѧ˼�룮
��������⣩
(1)����������֪ʶ�ⷽ�̣�(3x��5)2��4(3x��5)��3��0��
(2)����ABC������C��90�㣬����ֱ�DZߵij��ֱ�Ϊa��b��б�ߵij�Ϊc����(a2��b2)(a2��b2��1)��12����б��c�ij���
���𰸡���1����x1����![]() ��x2����
��x2����![]() .��2��
.��2��![]() .
.
����������1������3x��5��y��ԭ���̿��Ա�Ϊ��y24y��3��0���ٽ�һ������y�ķ������y��ֵ���ٷֱ����3x��5�Ϳ������x��ֵ�����ɵ�a2��b2��3����ֱ�����������ù��ɶ����ɵ�c��ֵ.
��2������a2��b2��x(x��0)����ԭ���̿ɻ�Ϊx(x��1)��12�����������x��һԪ���η��̣����x��ֵ��
(1)��3x��5��y����ԭ���̿ɱ���Ϊy2��4y��3��0�����y1��1��y2��3.
��y��1ʱ��3x��5��1�����x����![]() ��
��
��y��3ʱ��3x��5��3�����x����![]() ��
��
��x1����![]() ��x2����
��x2����![]() ��
��
(2)��a2��b2��x(x��0)����(a2��b2 )(a2��b2��1)��12�ɻ�Ϊx(x��1)��12��
��x2��x��12��0��
���x1��3��x2����4��0 (�������⣬��ȥ)��
��a2��b2��3.
�ߡ�C��90�㣬
��a2��b2��c2��
��c2��3��
��c��![]() .
.
��б��c�ij�Ϊ![]() .
.


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д� Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����A��O��B������ֱ��MN�ϣ��ֽ�����OA�Ƶ�O��˳ʱ�뷽����ÿ��4����ٶ���ת��ͬʱ����OB�Ƶ�O����ʱ�뷽����ÿ��6����ٶ���ת��ֱ��MN���ֲ�������ͼ2������תʱ��Ϊt(0��t��60����λ����)��
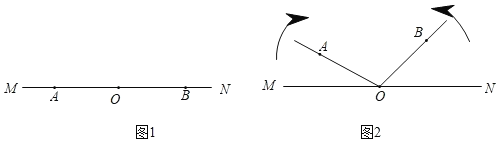
��1����t=3ʱ�����AOB�Ķ�����
��2�����˶������У�����AOB�ڶ��δﵽ72��ʱ����t��ֵ��
��3������ת�������Ƿ����������t��ʹ������OB������OA��ֱ��������ڣ������t��ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD��ֱ��MN��AB��CD�ֱ��ڵ�E��F��FGƽ�֡�EFD��EG��FG�ڵ�G������CFN��110�������BEG����������
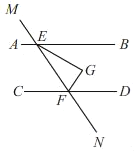
A. 20��B. 25��C. 35��D. 40��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ���ʵ��ķ��������з��̣�
(1)3(x��1)2��27����������(2)2x2��6��7x��
(3)3x(x��2)��2(2��x)������ (4)y2��4y��3��0.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
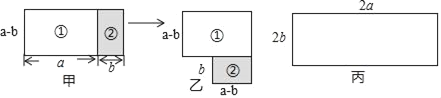
����Ŀ����ͼ��ʾ��ͼ���ɳ����٣���������ɣ�ͼ��ͨ���ƶ������ڵõ�ͼ�ң�
��1��S��=�� ����S��=�� �����ú�a��b�Ĵ���ʽ�ֱ��ʾ����
��2�����ã�1���Ľ����˵��a2��b2����a+b����a��b���ĵ�����ϵ��
��3������һ����ͼ���ߴ�ij�����ֽƬ����ͨ�������ָ�ٶԷָ�ĸ������ƶ�������µ�ͼ�Σ�����ͼ�Σ�����ͼ��˵����a+b��2����a��b��2��ab���ߵĵ�����ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֻ��1�����˶��ῪĻʽ����Ʊ��С����С�Ŷ���ȥ������������ȡתת�̣���ͼ��ת�����汻��Ϊ�����ȣ��ұ�������1��2��3��4��4������������Ϸ��ʽ����˭ʤ˭ȥ�ۿ����������£����˸�ת��ת��һ�Σ���ת��ָ��ֹͣ��������ָ���Ӧ�������ֶ�����������С��ʤ��������ָ���Ӧ�������ֶ���ż������С��ʤ��������ָ���Ӧ����������һ��һż����Ϊƽ�֣���Ϊƽ�֣�����������Ϸ��ֱ���ֳ�ʤ����
���С����С�Ű����������ת��ת��һ�Σ���
��1��С��ת��ת�̣���ת��ָ��ֹͣ����Ӧ��������Ϊ�����ĸ����Ƕ��٣�
��2������Ϸ�Ƿ�ƽ�������б�����״ͼ�ķ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����A=36����BEƽ�֡�ABC��DE//BC����ͼ�е��������ι��У� ����
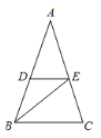
A. 3B. 4C. 5D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���AC��BD���ڵ�O��DEƽ�֡�ADC��AB�ڵ�E����BCD=60�㣬AD=![]() AB������OE�����н��ۣ���SABCD=ADBD����DBƽ�֡�CDE����AO=DE����S��ADE=5S��OFE��������ȷ�ĸ����У�������
AB������OE�����н��ۣ���SABCD=ADBD����DBƽ�֡�CDE����AO=DE����S��ADE=5S��OFE��������ȷ�ĸ����У�������
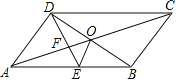
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���ax2+bx��1��0��a��0����һ��Ϊx��2019����һԪ���η���a��x��1��2+b��x��1����1����һ��Ϊ��������
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com