
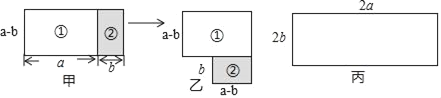
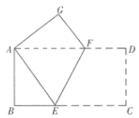
【题目】如图所示,图甲由长方形①,长方形②组成,图甲通过移动长方形②得到图乙.
(1)S甲= ,S乙= (用含a、b的代数式分别表示);
(2)利用(1)的结果,说明a2、b2、(a+b)(a﹣b)的等量关系;
(3)现有一块如图丙尺寸的长方形纸片,请通过对它分割,再对分割的各部分移动,组成新的图形,画出图形,利用图形说明(a+b)2、(a﹣b)2、ab三者的等量关系.
【答案】(1)(a+b)(ab);a2b2;(2)(a+b)(ab)=a2b2;(3)见解析
【解析】
(1)根据长方形的面积计算公式以及正方形的面积计算公式进行计算,即可得到结论;
(2)根据S甲=S乙即可得到a2、b2、(a+b)(ab)的等量关系;
(3)将图丙分成四个长为a,宽为b的小长方形,再拼成大正方形,即可得到(a+b)2、(a﹣b)2、ab三者的等量关系.
解:(1)由题可得,S甲=(a+b)(ab);
S乙=a2b2;
故答案为:(a+b)(ab);a2b2;
(2)∵S甲=S乙;
∴a2、b2、(a+b)(ab)的等量关系为:(a+b)(ab)=a2b2;
(3)如图①所示,将图丙分成四个长为a,宽为b的小长方形,再拼成如图②所示的正方形.
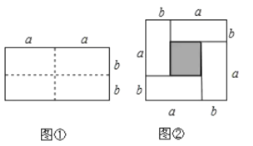
根据图②可得:
S大正方形=(a+b)2,
S大正方形=(ab)2+4ab,
∴(a+b)2=(ab)2+4ab.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
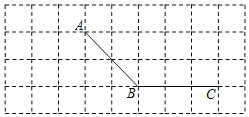
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
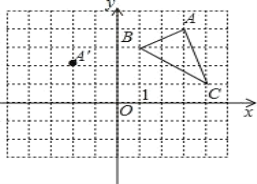
【题目】在平面直角坐标系中,△ABC 的三个顶点的位置如图所示,点 A′的坐标是(-2,2),现将△ABC 平移,使点 A 变换为点 A′,点 B′、C′分别是 B、C 的对应点.
(1) 请画出平移后的△A′B′C′(不写画法),并直接写出点B′、C′的坐标:B′ 、C′ ;
(2) 若△ABC 内部一点 P 的坐标为(![]() ,
,![]() ),则点 P 的对应点 P′的坐标是 ;
),则点 P 的对应点 P′的坐标是 ;
(3) 连接 A′B,CC′,并求四边形 A′BCC′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)解方程(x-1)2-5(x-1)+4=0时,我们发现:先将x-1看作一个整体,然后设x-1=y.……①,那么原方程可化为y2-5y+4=0,解得y1=1,y2=4.当y=1时,x-1=1,则x=2;当y=4时,x-1=4,则x=5,故原方程的解为x1=2,x2=5.
上述解题过程,在由原方程得到方程①的过程中,运用了“换元法”达到了解方程的目的,体现了转化的数学思想.
(解决问题)
(1)请利用以上知识解方程:(3x+5)2-4(3x+5)+3=0;
(2)在△ABC中,∠C=90°,两条直角边的长分别为a,b,斜边的长为c,且(a2+b2)(a2+b2+1)=12,求斜边c的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
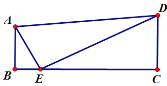
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,点E在BC边上,∠AED=90°
(1)求证:∠BAE=∠CED;(2)若AB+CD=DE,求证:AE+BE=CE
(3)在(2)的条件下,若△CDE与△ABE的面积的差为18,CD=6,求BE的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:要求尺规作图,不写作法,保留作图痕迹,写出结论。
(1)如图所示,104国道OA和327国道OB在曲阜市相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置;
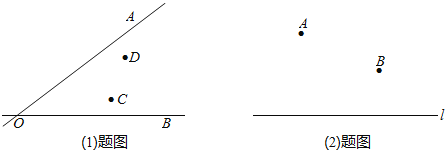
(2)在图中直线上找到一点M,使它到A、B两点的距离和最小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB= 4,BC= 8,将长方形纸片ABCD折叠,使点C恰好与A点重合,则折痕EF的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com