
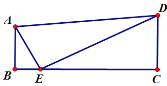
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,点E在BC边上,∠AED=90°
(1)求证:∠BAE=∠CED;(2)若AB+CD=DE,求证:AE+BE=CE
(3)在(2)的条件下,若△CDE与△ABE的面积的差为18,CD=6,求BE的长.


【答案】(1)见解析;(2)见解析;(3)3.
【解析】
(1)由∠AEB+∠CED=180°90°=90°,∠BAE+∠AEB=90°,即可得出结论;
(2)在ED上截取EF=AB,过点F作FG⊥DE交BC于G,连接DG,证出∠BAE=∠FEG,由ASA证得△ABE≌△EFG得出AE=EG,BE=FG,由AB+CD=DE,EF+DF=DE,得出DF=CD,由HL证得Rt△DFG≌Rt△DCG得出FG=CG,则BE=CG,即可得出结论;
(3)由△ABE≌△EFG,Rt△DFG≌Rt△DCG,得出S△ABE=S△EFG,S△DFG=S△DCG,则S△CDES△ABE=2S△CDG=18,得出S△CDG=9,则![]() CGCD=9,即可得出结果.
CGCD=9,即可得出结果.
(1)证明:∵∠AEB+∠CED=180°90°=90°,∠BAE+∠AEB=90°,
∴∠BAE=∠CED;
(2)证明:在ED上截取EF=AB,过点F作FG⊥DE交BC于G,连接DG,如图所示:
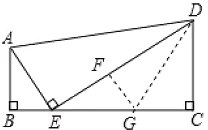
∵∠AEB+∠GEF=90°,∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
在△ABE和△EFG中,
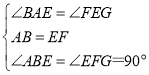 ,
,
∴△ABE≌△EFG(ASA),
∴AE=EG,BE=FG,
∵AB+CD=DE,EF+DF=DE,
∴DF=CD,
在Rt△DFG和Rt△DCG中,
![]() ,
,
∴Rt△DFG≌Rt△DCG(HL),
∴FG=CG,
∴BE=CG,
∴AE+BE=EG+CG=CE;
(3)解:∵△ABE≌△EFG,Rt△DFG≌Rt△DCG,
∴S△ABE=S△EFG,S△DFG=S△DCG,
∴S△CDES△ABE=2S△CDG=18,
∴S△CDG=9,
∴![]() CGCD=9,即
CGCD=9,即![]() ×CG×6=9,
×CG×6=9,
∴CG=BE=3.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,AC垂直平分BD,交BD于点F,延长DC到点E,使得CE=DC,连接BE.
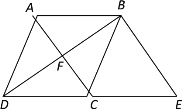
(1)求证:四边形ABCD是菱形.
(2)填空:
①当∠ADC= °时,四边形ACEB为菱形;
②当∠ADC=90°,BE=4时,则DE=
查看答案和解析>>
科目:初中数学 来源: 题型:
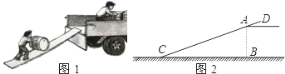
【题目】如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度?
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
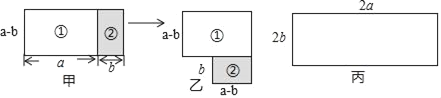
【题目】如图所示,图甲由长方形①,长方形②组成,图甲通过移动长方形②得到图乙.
(1)S甲= ,S乙= (用含a、b的代数式分别表示);
(2)利用(1)的结果,说明a2、b2、(a+b)(a﹣b)的等量关系;
(3)现有一块如图丙尺寸的长方形纸片,请通过对它分割,再对分割的各部分移动,组成新的图形,画出图形,利用图形说明(a+b)2、(a﹣b)2、ab三者的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
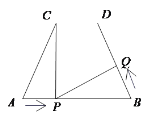
【题目】如图,AB=10cm,AC=BD=6cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
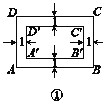
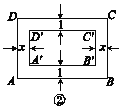
【题目】如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若在矩形ABCD的内部沿四周有宽为1的环形区域,矩形A′B′C′D′与矩形ABCD相似吗?请说明理由;
(2)如图②,当x为多少时,矩形ABCD与矩形A′B′C′D′相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() ,对角线
,对角线![]() 交于点
交于点![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
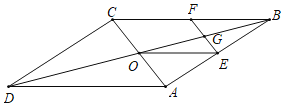
(1)证明:四边形![]() 是平行四边形
是平行四边形
(2)点![]() 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com