练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

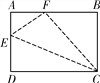
    【题目】如图，矩形ABCD中，AB＝10，BC＝8，E为AD边上一点，沿CE将△CDE对折，使点D正好落在AB边上F处，求tan∠AFE.

    【答案】

    【解析】根据题意，结合折叠的性质，易得∠AFE=∠BCF，进而在Rt△BFC中，有BC=8，CF=10，由勾股定理易得BF的长，根据三角函数的定义，易得tan∠BCF的值，借助∠AFE=∠BCF，可得tan∠AFE的值．

    解：根据折叠的性质，∠EFC＝∠EDC＝90°，

    即∠AFE＋∠BFC＝90°.

    又Rt△BCF中，∠BCF＋∠BFC＝90°，

    ∴∠AFE＝∠BCF.

    在Rt△BFC中，根据折叠的性质，有CF＝CD，BC＝8，

    CF＝CD＝10，由勾股定理易得BF＝6，则tan∠BCF＝，

    ∴tan∠AFE＝tan∠BCF＝

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，延长AB至E，延长CD至F，BE=DF，连接EF，与BC、AD分别相交于P、Q两点．

    （1）求证：CP=AQ；

    （2）若BP=1，PQ=，∠AEF=45°，求矩形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某村耕地总面积为50公顷，且该村人均耕地面积y（单位：公顷/人）与总人口x（单位：人）的函数图象如图所示，则下列说法正确的是（ ）

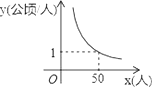
    A. 该村人均耕地面积随总人口的增多而增多

    B. 该村人均耕地面积y与总人口x成正比例

    C. 若该村人均耕地面积为2公顷，则总人口有100人

    D. 当该村总人口为50人时，人均耕地面积为1公顷

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，直线MN与AB、CD分别交于点E、F，FG平分∠EFD，EG⊥FG于点G，若∠CFN＝110°，则∠BEG＝（　　）

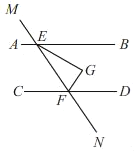
    A. 20°B. 25°C. 35°D. 40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

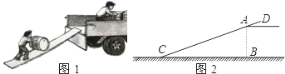
    【题目】如图1是工人将货物搬运上货车常用的方法，把一块木板斜靠在货车车厢的尾部，形成一个斜坡，货物通过斜坡进行搬运．根据经验，木板与地面的夹角为20°(即图2中∠ACB＝20°)时最为合适，已知货车车厢底部到地面的距离AB＝1.5m，木板超出车厢部分AD＝0.5m，请求出木板CD的长度？

    (参考数据：sin20°≈0.3420，cos20°≈0.9397，精确到0.1m)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】选择适当的方法解下列方程：

    (1)3(x＋1)2＝27；　　　　(2)2x2＋6＝7x；

    (3)3x(x－2)＝2(2－x)；　　 (4)y2－4y－3＝0.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

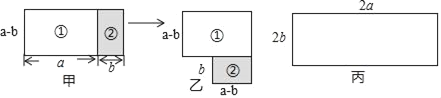
    【题目】如图所示，图甲由长方形①，长方形②组成，图甲通过移动长方形②得到图乙．

    （1）S甲=　 　，S乙=　 　（用含a、b的代数式分别表示）；

    （2）利用（1）的结果，说明a2、b2、（a+b）（a﹣b）的等量关系；

    （3）现有一块如图丙尺寸的长方形纸片，请通过对它分割，再对分割的各部分移动，组成新的图形，画出图形，利用图形说明（a+b）2、（a﹣b）2、ab三者的等量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ΔABC中，AB=AC，∠A=36°，BE平分∠ABC，DE//BC，则图中等腰三角形共有（ ）个

    A. 3B. 4C. 5D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代对于利用方程解决实际问题早有研究，《九章算术》中提到这么一道“以绳测井”的题：以绳测井，若将绳三折测之，绳多四尺：若将绳四折测之，绳多一尺．绳长、井深各几何？

    这道题大致意思是：用绳子测量水井深度，如果将绳子折成三等份，那么每等份井外余绳四尺：如果将绳子折成四等份，那么每等份井外余绳一尺．问绳长和井深各多少尺？若设井深为x尺，则求解井深的方程正确的是（　　）

    A.3（x+4）＝4（x+1）B.3x+4＝4x+1

    C.x+4＝x+1D.x﹣4＝x﹣1

    查看答案和解析>>

    同步练习册答案