
����Ŀ���ҹ��Ŵ��������÷��̽��ʵ�����������о������������������ᵽ��ôһ���������⾮�����⣺�����⾮�����������۲�֮�������ijߣ����������۲�֮������һ�ߣ���������������Σ�
����������˼�ǣ������Ӳ���ˮ����ȣ�����������۳����ȷݣ���ôÿ�ȷݾ��������ijߣ�����������۳��ĵȷݣ���ôÿ�ȷݾ�������һ�ߣ��������;�������ٳߣ����辮��Ϊx�ߣ�����⾮��ķ�����ȷ���ǣ�������
A.3��x+4����4��x+1��B.3x+4��4x+1
C.![]() x+4��
x+4��![]() x+1D.
x+1D.![]() x��4��
x��4��![]() x��1
x��1
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�����һ���·���������![]() Ԫ�����п����ǰ�
Ԫ�����п����ǰ�![]() Ԫ�����ģ�ӯ����
Ԫ�����ģ�ӯ����![]() �����¿�����
�����¿�����![]() ����
����
��1�������·��п��ӵĽ����Ƕ���Ԫ��
��2�������·��������ǰ�����Ԫ�����ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��
��![]() �������϶�Ӧ����Ϊ
�������϶�Ӧ����Ϊ![]() ��
��![]() �����
�����![]() ��
��![]() ��
��![]() ֮��ľ��룬����
֮��ľ��룬����![]() .��֪����������
.��֪����������![]() ��
��![]() ��Ӧ�����ֱ�Ϊ
��Ӧ�����ֱ�Ϊ![]() ��
��![]() ��������
��������![]() ����
����![]() Ϊ������һ���㣬���Ӧ����Ϊ
Ϊ������һ���㣬���Ӧ����Ϊ![]() .
.
��1������![]() ����
����![]() ��
��![]() �ľ�����ȣ����
�ľ�����ȣ����![]() ��Ӧ������_________.
��Ӧ������_________.
��2���������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������ڣ������
�������ڣ������![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
��3������![]() ��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶�ʱ����
��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶�ʱ����![]() ��ÿ��3����λ���������˶�����
��ÿ��3����λ���������˶�����![]() ��ÿ��15����λ���������˶���������ͬʱ�����������Ӻ��
��ÿ��15����λ���������˶���������ͬʱ�����������Ӻ��![]() ����
����![]() ��
��![]() �ľ�����ȣ�
�ľ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��

��1����֤��AB=CF��
��2������DE����AD=2AB����֤��DE��AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD����DE��CE������AE���ӳ���BC���ӳ����ڵ�F.
(1)��֤����ADE�ա�FCE��
(2)��AB��2BC����F��36�������B�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() �ľŸ�����������
�ľŸ�����������![]() �����֣� ��ÿ�С�ÿ�м�ÿ���Խ��ߵ�
�����֣� ��ÿ�С�ÿ�м�ÿ���Խ��ߵ�![]() ������֮�Ͷ����ʱ�����ǰ�����ͼ��֮Ϊ�Ź���λͼ:
������֮�Ͷ����ʱ�����ǰ�����ͼ��֮Ϊ�Ź���λͼ:
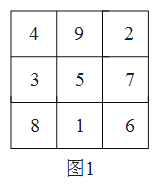
��1����![]() ����
����![]() ����Ҳ�ܹ��ɾŹ���λͼ�� ���ʱÿ�С�ÿ�м�ÿ���Խ��ߵ�
����Ҳ�ܹ��ɾŹ���λͼ�� ���ʱÿ�С�ÿ�м�ÿ���Խ��ߵ�![]() ������֮�Ͷ�Ϊ ��
������֮�Ͷ�Ϊ ��
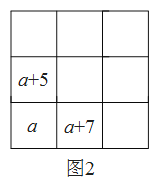
��2����ͼ2.�����žŹ���λͼ�У�ֻ������![]() �������뽫ʣ���
�������뽫ʣ���![]() ����ֱ�������2�У�(�ú�
����ֱ�������2�У�(�ú�![]() �Ĵ���ʽ�ֱ��ʾ��
�Ĵ���ʽ�ֱ��ʾ��![]() ����)
����)
��3����ͼ3�������žŹ���λͼ�У�ֻ������![]() ����������������Ͻǡ�
����������������Ͻǡ�![]() ������ʾ����ֵ.
������ʾ����ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
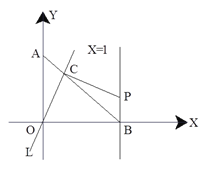
����Ŀ����ͼ����A��y���ϣ���B��x���ϣ���OA=OB=1������ԭ��O��ֱ��![]() ���߶�AB�ڵ�C����C��OC�Ĵ��ߣ���ֱ��x=1�ཻ�ڵ�P���ֽ�ֱ��
���߶�AB�ڵ�C����C��OC�Ĵ��ߣ���ֱ��x=1�ཻ�ڵ�P���ֽ�ֱ��![]() ��O����ת��ʹ����C��A��B�˶�����C������ڵ�һ�����ڣ�����AC�ij�Ϊt��������ͼ��������������̽����
��O����ת��ʹ����C��A��B�˶�����C������ڵ�һ�����ڣ�����AC�ij�Ϊt��������ͼ��������������̽����
��1������AOC����BCPȫ��ʱ�����t��ֵ��
��2��ͨ�����ֲ����߶�OC��CP�ij����ж�����֮��Ĵ�С��ϵ����֤����õ��Ľ��ۡ�
��3�������P������Ϊ��1,b��,��д��b����t�ĺ�����ϵʽ�ͱ���t��ȡֵ��Χ�����������PBCΪ����������ʱ��P�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�У�AB//CD��AC//BD�������ж�����ȷ���� ( )
A. ���BC=AD����ô�ı���ABCD�ǵ������Σ�
B. ���AD//BC����ô�ı���ABCD�����Σ�
C. ���ACƽ��BD����ô�ı���ABCD�Ǿ��Σ�
D. ���AC��BD����ô�ı���ABCD��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ŵ��������������ͣ���ͼ1��ʾ��������6m�����20m��������֧����ľ����Ϊ5m��
��1���������߷���������ֱ������ϵ�У���ͼ2��ʾ���������ʽ��y=ax2+c����ʽ��������������������a��c��ֵ��
��2����֧��MN�ij��ȣ�
��3�������µ�ƽ����˫���г��������м���һ����2m�ĸ�����������е�һ���г����ܷ�����ʻ��2m����3m������������������ļ�����Բ��ƣ�����˵˵������ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com