
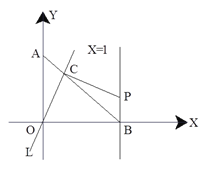
����Ŀ����ͼ����A��y���ϣ���B��x���ϣ���OA=OB=1������ԭ��O��ֱ��![]() ���߶�AB�ڵ�C����C��OC�Ĵ��ߣ���ֱ��x=1�ཻ�ڵ�P���ֽ�ֱ��
���߶�AB�ڵ�C����C��OC�Ĵ��ߣ���ֱ��x=1�ཻ�ڵ�P���ֽ�ֱ��![]() ��O����ת��ʹ����C��A��B�˶�����C������ڵ�һ�����ڣ�����AC�ij�Ϊt��������ͼ��������������̽����
��O����ת��ʹ����C��A��B�˶�����C������ڵ�һ�����ڣ�����AC�ij�Ϊt��������ͼ��������������̽����
��1������AOC����BCPȫ��ʱ�����t��ֵ��
��2��ͨ�����ֲ����߶�OC��CP�ij����ж�����֮��Ĵ�С��ϵ����֤����õ��Ľ��ۡ�
��3�������P������Ϊ��1,b��,��д��b����t�ĺ�����ϵʽ�ͱ���t��ȡֵ��Χ�����������PBCΪ����������ʱ��P�����ꡣ
���𰸡�(1) t=![]() ��(2)��������(3) P��1.1��, P��1��1��
��(2)��������(3) P��1.1��, P��1��1��![]() ��
��
��������������
��1������֪������OA=OB=1��AB=![]() ������AOC����BCPȫ�ȿɵ�BC=OA=1���Ӷ��ɵ�t=AC=AB-BC=
������AOC����BCPȫ�ȿɵ�BC=OA=1���Ӷ��ɵ�t=AC=AB-BC=![]() ��
��
��2������C��x���ƽ���߽�OA�ڵ�M����PB�ڵ�N����������OM=BN=CN����OMC=��CNP=90�㣬��COM=��PCN���ɴ˿ɵá�OMC�ա�CNP���Ӷ��ɵ�OC=PC��
��3�����ɡ�OMC�ա�CNP���ɵ�PN=MC=AM�����AM=sin45��![]() AC=
AC=![]() ���ɴ˿ɵ�BN=OM=1-AM=
���ɴ˿ɵ�BN=OM=1-AM=![]() ���Ӷ��ɵ�PB=b=BN-PN=
���Ӷ��ɵ�PB=b=BN-PN=![]() ����b=
����b=![]() ���ɵ�C�ڵ�һ���ɵ�t��ȡֵ��Χ�ǣ�
���ɵ�C�ڵ�һ���ɵ�t��ȡֵ��Χ�ǣ�![]() �������ݵ�Cֻ���ڵ�һ���ޣ���������PC=PB��PB=BC����������ۼ��㼴��.
�������ݵ�Cֻ���ڵ�һ���ޣ���������PC=PB��PB=BC����������ۼ��㼴��.
��⣺
��1����OA=OB=1����AOB=90�㣬
��AB=![]() ��
��
�ߡ�AOC����BCPȫ����
��BC=OA=1��
��AC=AB-BC=![]() ����
����![]() ��
��
��2������C��x���ƽ���߽�OA�ڵ�M����PB�ڵ�N��
���CMO=��OCP=��CNB=90�㣬
���ı���OBNM�Ǿ��Σ���MOC+��MCO=90�㣬��MCO+��NCP=90�㣬
��BN=OM����MOC=��NCP��
��OA=OB=1,
���BAO=��ABO=��ABN=45�㣬
���BCN�ǵ���ֱ����������
��OM=BN=CN��
���MOC�ա�NCP��
��OC=PC��
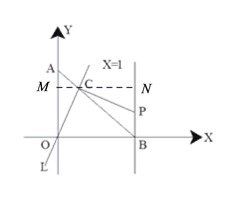
��3���� ��OA=OB=1,��AOB=90�㣬
���BAO=��ABO=45�㣬
���ߡ�AMC=90�㣬
��AM=MC=AC��sin45��=![]() ��
��
��OM=OA-AM=![]() ��
��
������2����֪��BN=OM��
��NB=![]() ,
,
�ߡ�AOC����BCPȫ����
��PN=CM=AM=![]() ��
��
��PB=BN-PN=![]() ����b=
����b=![]() ��
��
����C�ڵ�һ���ޣ�
��![]() ��
��
����t=0ʱ����PBC�ǵ���ֱ�������Σ�����ʱ��C���A�غϣ����ڵ�һ���ޣ�����������Ҫ�ʴ��������������
��PB=BCʱ���ɣ�2����֪![]() �����t=1��t=-1����ȥ����
�����t=1��t=-1����ȥ����
����t=1ʱ����PBC�ǵ��������Σ���ʱ��P������Ϊ![]() ��
��
��������������PBCΪ����������ʱ����P������Ϊ![]() .
.


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻͬѧ�Ŀ���������ijѧУ��������������Ȼ���������������ȡ�˲���ѧ����������Ϊ��������ȥ�ľ�����________�����ʾ�������Ҫ��ѧ��ֻ�ܴ���A���̲�����B����������C��ʪ�ع�����D��ɭ�ֹ������ĸ�������ѡ��һ�������ݵ�����������������������������ͳ��ͼ��

�ش�����������
��1�����ι������˶�����ѧ����
��2����ȫ����ͳ��ͼ��
��3������ѧУ����3 600��ѧ�����Թ��Ƹ�Уȥʪ�ع���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����м�����̣�����������.
![]() =1
=1 ![]() =8
=8 ![]() =27
=27 ![]() =64
=64 ![]() =125
=125 ![]() =216
=216 ![]() =343
=343 ![]() =512
=512 ![]() =729
=729
��1��С�������������19683���������ģ��ȹ���19683���������ĸ�λ��, �������ĸ�λ��Ϊ , ����![]() <19000<
<19000< ![]() ������19683��������ʮλ��Ϊ ����֤��19683���������� .
������19683��������ʮλ��Ϊ ����֤��19683���������� .
��2��������ݣ�1����С���ķ��������������գ�
�� ![]() = �� ��
= �� ��![]() = ����
= ����![]() = .
= .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ��������÷��̽��ʵ�����������о������������������ᵽ��ôһ���������⾮�����⣺�����⾮�����������۲�֮�������ijߣ����������۲�֮������һ�ߣ���������������Σ�
����������˼�ǣ������Ӳ���ˮ����ȣ�����������۳����ȷݣ���ôÿ�ȷݾ��������ijߣ�����������۳��ĵȷݣ���ôÿ�ȷݾ�������һ�ߣ��������;�������ٳߣ����辮��Ϊx�ߣ�����⾮��ķ�����ȷ���ǣ�������
A.3��x+4����4��x+1��B.3x+4��4x+1
C.![]() x+4��
x+4��![]() x+1D.
x+1D.![]() x��4��
x��4��![]() x��1
x��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ļ��ڿ�Ļǰ��ij��˲�Ҷ��˾Ԥ������˲�Ҷ�ܹ�����������32000Ԫ������һ����˲�Ҷ�����к�ܿ���������Ҷ��˾����68000Ԫ�����ڶ�����˲�Ҷ�����������ǵ�һ������������2������ÿǧ�˷�˲�Ҷ���۶���10Ԫ��
��1���÷�˲�Ҷ��˾���ι��������ַ�˲�Ҷ����ǧ�ˣ�
��2�������������Ҷÿǧ�˵��ۼ���ͬ����ȫ��������������ʲ�����20%����ôÿǧ���ۼ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�2014��ij����10�������С�Сѧ��50���ܳɼ�������������Ŵ�������ѧ��Ⱥ���и���ȡ��10%��ѧ�����м�⣬�����������ݣ������2010�����������õ�����ͳ��ͼ��
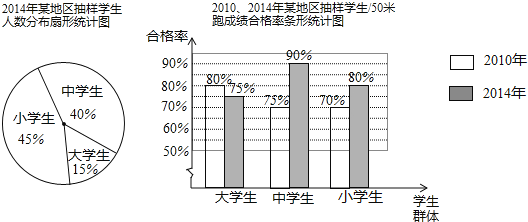
��1�����μ���ȡ�˴��С�Сѧ������ ����������Сѧ���� ������
��2�����ݳ����Ľ��������2014��õ���10�������С�Сѧ���У�50���ܳɼ��ϸ����ѧ������Ϊ�� ������
��3���Ƚ�2010����2014�����ѧ��50���ܳɼ��ϸ��������д��һ����ȷ�Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
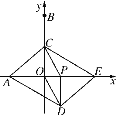
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ���(��3��0)��(0��6)������P�ӵ�O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�����CP��COΪ�ڱ߹���PCOD.���߶�OP�ӳ�����һ����E��������PE��AO.
(1)����C���߶�OB���˶�ʱ����֤���ı���ADECΪƽ���ı��Σ�
(2)����P�˶���ʱ��Ϊ![]() ��ʱ�����ʱ�ı���ADEC���ܳ��Ƕ��٣�
��ʱ�����ʱ�ı���ADEC���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ��������ACD����ACD=90����AC=![]() ���ֱ��Ա�AD��AC��CDΪֱ�����ͼ��������������ͼ��AGCE��DHCF�����֮��(ͼ����Ӱ����)Ϊ_____________��
���ֱ��Ա�AD��AC��CDΪֱ�����ͼ��������������ͼ��AGCE��DHCF�����֮��(ͼ����Ӱ����)Ϊ_____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬����
��һ�㣬����![]() ������
������![]() ��ʹ
��ʹ![]() ����һֱ�����ǰ��ֱ�Ƕ�����ڵ�
����һֱ�����ǰ��ֱ�Ƕ�����ڵ�![]() ����һ��
����һ��![]() ������
������![]() �ϣ���һ��
�ϣ���һ��![]() ��ֱ��
��ֱ��![]() ���Ϸ�.
���Ϸ�.
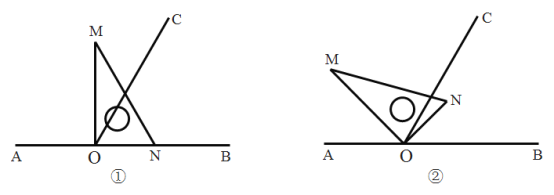
��1����ͼ���У�![]() __________�ȣ�
__________�ȣ�
��2����ͼ���е����ǰ��Ƶ�![]() ����ʱ�뷽����ת��ʹ��
����ʱ�뷽����ת��ʹ��![]() ��
��![]() ���ڲ�����ͼ�ڣ���
���ڲ�����ͼ�ڣ���![]() ����
����![]() �Ķ�����
�Ķ�����
��3����ͼ���е����ǰ��Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���ֱ��
���ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���ֱ��![]() ǡ��ƽ�����
ǡ��ƽ�����![]() ʱ����ת��ʱ����__________��.��ֱ��д�������
ʱ����ת��ʱ����__________��.��ֱ��д�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com