
����Ŀ������![]() ��
��![]() �������϶�Ӧ����Ϊ
�������϶�Ӧ����Ϊ![]() ��
��![]() �����
�����![]() ��
��![]() ��
��![]() ֮��ľ��룬����
֮��ľ��룬����![]() .��֪����������
.��֪����������![]() ��
��![]() ��Ӧ�����ֱ�Ϊ
��Ӧ�����ֱ�Ϊ![]() ��
��![]() ��������
��������![]() ����
����![]() Ϊ������һ���㣬���Ӧ����Ϊ
Ϊ������һ���㣬���Ӧ����Ϊ![]() .
.
��1������![]() ����
����![]() ��
��![]() �ľ�����ȣ����
�ľ�����ȣ����![]() ��Ӧ������_________.
��Ӧ������_________.
��2���������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������ڣ������
�������ڣ������![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
��3������![]() ��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶�ʱ����
��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶�ʱ����![]() ��ÿ��3����λ���������˶�����
��ÿ��3����λ���������˶�����![]() ��ÿ��15����λ���������˶���������ͬʱ�����������Ӻ��
��ÿ��15����λ���������˶���������ͬʱ�����������Ӻ��![]() ����
����![]() ��
��![]() �ľ�����ȣ�
�ľ�����ȣ�
���𰸡���1��1����2��-3��5����3��![]() ��
��![]()
��������
��1���ȸ��ݷǸ��Եõ�a,b��ֵ���ٸ����е�����ʼ�����⣻
��2������������������������⣻
��3����������ֵ���![]() δ�ϵ�
δ�ϵ�![]() ʱ�͵���
ʱ�͵���![]() �ϵ�
�ϵ�![]() ��
��![]() ��
��![]() �غ�ʱ���ֱ������⼴��.
�غ�ʱ���ֱ������⼴��.
��1����![]()
��a=-2��b=4
������������![]() ��
��![]() ��Ӧ�����ֱ�Ϊ-2��4��
��Ӧ�����ֱ�Ϊ-2��4��
�ߵ�![]() ����
����![]() ��
��![]() �ľ������
�ľ������
��P���ʾ����Ϊ![]()
���1��
��2�����������
������![]() �ڵ�
�ڵ�![]() �����ʱ
�����ʱ
![]()
��ã�![]()
������![]() �ڵ�
�ڵ�![]() ���Ҳ�ʱ
���Ҳ�ʱ
![]()
��ã�![]()
��3����![]() ����
����![]() ����
����![]() ��
��![]() �ľ������
�ľ������
��![]() ���
���![]() ��ʾ����Ϊ
��ʾ����Ϊ![]()
��![]() ��ʾ����Ϊ
��ʾ����Ϊ![]()
��![]() ��ʾ����Ϊ
��ʾ����Ϊ![]()
������![]() δ�ϵ�
δ�ϵ�![]() ʱ
ʱ
![]()
��ã�![]()
������![]() �ϵ�
�ϵ�![]() ��
��![]() ��
��![]() �غ�ʱ
�غ�ʱ
![]()
��ã�![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� ![]() ABCD�У���DAB��60�㣬��E��F�ֱ���CD��AB���ӳ����ϣ���AE��AD��CF��CB��
ABCD�У���DAB��60�㣬��E��F�ֱ���CD��AB���ӳ����ϣ���AE��AD��CF��CB��
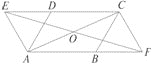
��1����֤���ı���AFCE��ƽ���ı��Σ�
��2����ȥ����֪�����ġ���DAB��60�㣬�����Ľ��ۻ������� ������������д��֤�����̣�������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����뾶Ϊ2��Բ�Ľ�Ϊ120�������OAB�Ƶ�A��ʱ����ת60�㣬��O��B�Ķ�Ӧ��ֱ�ΪO�䣬B�䣬����BB�䣬��ͼ����Ӱ���ֵ�����ǣ� �� 
A.![]()
B.2 ![]() ��
�� ![]()
C.2 ![]() ��
�� ![]()
D.4 ![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() �����
�����![]() ��
��![]() ����ô
����ô![]() �ij�Ϊ________
�ij�Ϊ________![]() ��
��![]() �ij�Ϊ_______
�ij�Ϊ_______![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶġ���![]() ��
��![]() ���ϵĸ��ߡ��ij߹���ͼ����.
���ϵĸ��ߡ��ij߹���ͼ����.
��֪��![]() .
.
������![]() ��
��![]() ���ϵĸ���
���ϵĸ���![]() .
.
��������ͼ��
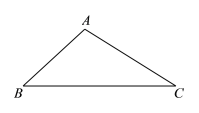
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶�������Ե�
�ij�Ϊ�뾶�������Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶������������
�ij�Ϊ�뾶������������![]() �·����ڵ�
�·����ڵ�![]() ��
��
������![]() ��
��![]() �ڵ�
�ڵ�![]() .
.
�����߶�![]() ��
��![]() ��
��![]() ���ϵĸ���.
���ϵĸ���.
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤��.
֤�������� ![]() ����
���� ![]() ��
��
���![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() �Ĵ�ֱƽ�����ϣ��� ���������������ݣ�.
�Ĵ�ֱƽ�����ϣ��� ���������������ݣ�.
��![]() ��ֱƽ���߶�
��ֱƽ���߶�![]() .
.
���߶�![]() ��
��![]() ��
��![]() ���ϵĸ���.
���ϵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����С��ͬ�������ſ飬����涼�ǵȱ������Σ�С�����α߳��Ǵ������α߳���һ�룬��O��С�����ε����ģ��ֽ�С���������Ŵ������εı�Ե˳ʱ����������ɢ�λ�ù�������λ��ʱ���߶�OA�Ƶ�O˳ʱ��ת���ĽǶ��ǣ� �� 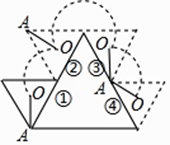
A.240��
B.360��
C.480��
D.540��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���ϵ�һ������(�����
���ϵ�һ������(�����![]() ��
��![]() ��
��![]() �е��غ�)������
�е��غ�)������![]() ����
����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�Ϊ��
�ĶԳƵ�Ϊ��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
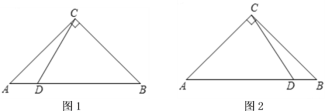
��1����ͼ1����![]() ʱ���������⽫ͼ�β�����������ֱ��д��
ʱ���������⽫ͼ�β�����������ֱ��д��![]() �Ķ�����
�Ķ�����
��2����ͼ2����![]() ʱ���õ�ʽ��ʾ�߶�
ʱ���õ�ʽ��ʾ�߶�![]() ��
��![]() ��
��![]() ֮���������ϵ��������֤��.
֮���������ϵ��������֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=kx+b������A��5��0����B��1��4����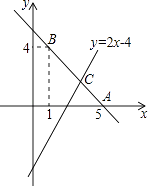
��1����ֱ��AB�Ľ���ʽ��
��2����ֱ��y=2x��4��ֱ��AB�ཻ�ڵ�C�����C�����ꣻ
��3������ͼ��д������x�IJ���ʽ2x��4��kx+b�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
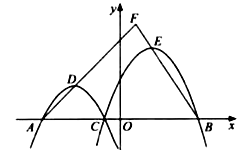
����Ŀ����ͼ����ƽ��ֱ������ϵ ![]() �У���֪
�У���֪ ![]() ��
�� ![]() ���������ֱ�Ϊ
���������ֱ�Ϊ ![]() ��
�� ![]() ��
�� ![]() ���߶�
���߶� ![]() ��һ�㣨��
��һ�㣨�� ![]() ��
�� ![]() �㲻�غϣ���������
�㲻�غϣ��������� ![]()
![]() ��
�� ![]() ��������
�������� ![]() ��
�� ![]() ������Ϊ
������Ϊ ![]() ��������
�������� ![]()
![]() ��
�� ![]() ��������
�������� ![]() ��
�� ![]() ������Ϊ
������Ϊ ![]() ��
�� ![]() ��
�� ![]() ���ӳ����ཻ�ڵ�
���ӳ����ཻ�ڵ� ![]() ��
��
��1���� ![]() ��
�� ![]() ����������
���������� ![]() ��
�� ![]() �Ľ���ʽ��
�Ľ���ʽ��
��2���� ![]() ��
�� ![]() ����
���� ![]() ��ֵ��
��ֵ��
��3���Ƿ����������ʵ�� ![]() ��
�� ![]() ��������
�������� ![]() ȡ��ֵ��ֱ��
ȡ��ֵ��ֱ�� ![]() ��
�� ![]() �������ܻ��ഹֱ�������ڣ���ֱ��д��
�������ܻ��ഹֱ�������ڣ���ֱ��д�� ![]() ��������ͬ��ֵ���������ڣ���˵�����ɣ�
��������ͬ��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com