
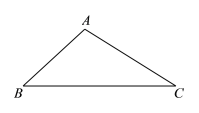
����Ŀ��������С����Ƶġ���![]() ��
��![]() ���ϵĸ��ߡ��ij߹���ͼ����.
���ϵĸ��ߡ��ij߹���ͼ����.
��֪��![]() .
.
������![]() ��
��![]() ���ϵĸ���
���ϵĸ���![]() .
.
��������ͼ��
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶�������Ե�
�ij�Ϊ�뾶�������Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶������������
�ij�Ϊ�뾶������������![]() �·����ڵ�
�·����ڵ�![]() ��
��
������![]() ��
��![]() �ڵ�
�ڵ�![]() .
.
�����߶�![]() ��
��![]() ��
��![]() ���ϵĸ���.
���ϵĸ���.
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤��.
֤�������� ![]() ����
���� ![]() ��
��
���![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() �Ĵ�ֱƽ�����ϣ��� ���������������ݣ�.
�Ĵ�ֱƽ�����ϣ��� ���������������ݣ�.
��![]() ��ֱƽ���߶�
��ֱƽ���߶�![]() .
.
���߶�![]() ��
��![]() ��
��![]() ���ϵĸ���.
���ϵĸ���.
���𰸡���1������������2��������
��������
��1�����ü������Ի�����Ӧ�ļ���ͼ�Σ�
��2��ͨ����ͼ�õ�AM=AN��MP=NP��������߶δ�ֱƽ���ߵ����ʶ������涨�����ж�AP���߶�MN�Ĵ�ֱƽ���ߣ��Ӷ��õ�AD��BC��
��1����ȷ��ȫͼ�Σ�
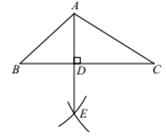
��2��֤������AM=AN��MP=NP��
��AP���߶�MN�Ĵ�ֱƽ���ߣ���һ���߶������˵������ȵĵ��������߶εĴ�ֱƽ�����ϣ�
��AD��BC��D�����߶�ADΪ��ABC�ı�BC�ϵĸߣ�
�ʴ�ΪAN��NP����һ���߶������˵������ȵĵ��������߶εĴ�ֱƽ�����ϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ȷֳ��Ŀ�С�����Σ�Ȼ��ͼ����״ƴ��һ�������Σ�
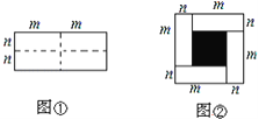
��1������Ϊͼ���е���Ӱ���ֵ������εı߳�����________��
��2���������ֲ�ͬ�ķ�����ͼ������Ӱ���ֵ�����������û���
����1��___________������2��___________��
��3�������⣨2������д����������ʽ��![]() ��
��![]() ��mn֮���һ��������ϵ��
��mn֮���һ��������ϵ��
��______________��
��4�����ݣ�3�����еĵ�����ϵ����ȫƽ����ʽ������������⣺
����֪��m+n��5��mn����3����m��n��2��ֵ��
����֪m��n��5��![]() ����mn��ֵ��
����mn��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BO��CO�ֱ�ƽ�֡�ABC����ACB������BOC=110�������A=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CD�ǡ�O��ֱ������EOD=72�㣬AE����O�ڵ�B����AB=OC�����A�Ķ�����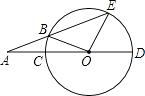
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼʾ������ABC��һ��P�����PAC=��PBA=��PCB�����PΪ��ABC�IJ��忨�㣮�����εIJ��忨�㣨Brocard point���Ƿ�����ѧ�Һ���ѧ�����ҿ������A��L��Crelle 1780��1855����1816���״η��֣������ķ��ֲ�δ����ʱ��������ע�⣬1875�꣬���忨�㱻һ����ѧ�����߷������ٲ��忨��Brocard 1845��1922�����·��֣����������������������⣺��֪�ڵ���ֱ��������DEF�У���EDF=90�㣬����QΪ��DEF�IJ��忨�㣬DQ=1����EQ+FQ=�� �� 
A.5
B.4
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��
��![]() �������϶�Ӧ����Ϊ
�������϶�Ӧ����Ϊ![]() ��
��![]() �����
�����![]() ��
��![]() ��
��![]() ֮��ľ��룬����
֮��ľ��룬����![]() .��֪����������
.��֪����������![]() ��
��![]() ��Ӧ�����ֱ�Ϊ
��Ӧ�����ֱ�Ϊ![]() ��
��![]() ��������
��������![]() ����
����![]() Ϊ������һ���㣬���Ӧ����Ϊ
Ϊ������һ���㣬���Ӧ����Ϊ![]() .
.
��1������![]() ����
����![]() ��
��![]() �ľ�����ȣ����
�ľ�����ȣ����![]() ��Ӧ������_________.
��Ӧ������_________.
��2���������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������ڣ������
�������ڣ������![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
��3������![]() ��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶�ʱ����
��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶�ʱ����![]() ��ÿ��3����λ���������˶�����
��ÿ��3����λ���������˶�����![]() ��ÿ��15����λ���������˶���������ͬʱ�����������Ӻ��
��ÿ��15����λ���������˶���������ͬʱ�����������Ӻ��![]() ����
����![]() ��
��![]() �ľ�����ȣ�
�ľ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD����CAE��90�㣬AB��AD��AE��AC.
(1)֤����BC=DE��
(2)��AC��12�����ı���ABCD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾������ 960 ���²�Ʒ��Ҫ���ӹ�����Ͷ���г����ּס���������������ӹ�������Ʒ����֪���������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ���� 20 �죬������ÿ��ӹ����������ҹ���ÿ��ӹ���������![]() ����˾�踶�����ӹ�����Ϊÿ�� 80 Ԫ���ҹ����ӹ�����Ϊÿ�� 120 Ԫ��
����˾�踶�����ӹ�����Ϊÿ�� 80 Ԫ���ҹ����ӹ�����Ϊÿ�� 120 Ԫ��
��1���ס�����������ÿ����ܼӹ����ټ��²�Ʒ��
��2����˾�ƶ���Ʒ�ӹ��������£�������ÿ�����ҵ�����ɣ�Ҳ�������������Һ�����ɣ��ڼӹ������У���˾��һ������ʦÿ�쵽�����м���ָ����������ÿ�� 15 Ԫ����Ͳ����ѣ� ����﹫˾ѡ��һ�ּ�ʡʱ��ʡǮ�ļӹ���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У� A��B����ֱ���x�ᡢy����������ϣ���OB = OA=3����1�������A��B�����ꣻ��2������֪��C����2��2��������BOC���������3������P�ǵ�һ����ƽ������һ�㣬��![]() �����P�����꣮
�����P�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com