
【题目】如图①是一个长为2m.宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.
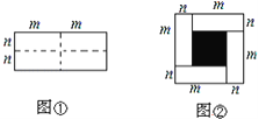
(1)你认为图②中的阴影部分的正方形的边长等于________?
(2)请用两种不同的方法求图②中阴影部分的面积.(不用化简)
方法1:___________;方法2:___________.
(3)由问题(2)你能写出三个代数式:![]() ,
,![]() ,mn之间的一个等量关系.
,mn之间的一个等量关系.
答:______________.
(4)根据(3)题中的等量关系和完全平方公式,解决如下问题:
①已知:m+n=5,mn=-3,求:(m﹣n)2的值;
②已知m-n=5,![]() ,求mn的值.
,求mn的值.
【答案】(1)![]() ;(2)
;(2)![]() ;
;![]() ;(3)
;(3)![]() ;(4)①37;②47.
;(4)①37;②47.
【解析】
(1)根据拼图的方式即可得出阴影部分的正方形的边长;
(2)根据面积公式以及间接法,即可得到图②中阴影部分的面积的不同代数式;
(3)根据两种不同的方法表示图②中阴影部分的面积相等,即可得到(m+n)2、(m﹣n)2、mn之间的等量关系;
(4)①利用(3)中的等量关系,把m+n=5,mn=-3代入计算即可;
②由完全平方差公式变形,再把m-n=5,![]() 代入计算即可.
代入计算即可.
(1)由题意可知:图②中的阴影部分的正方形的边长为m-n;
(2)由题意可知:两种不同的方法表示图②中阴影部分的面积分别为:
方法1:![]() ;方法2:
;方法2:![]() ;
;
(3)由问题(2)可知:![]() ;
;
(4)①解:∵m+n=5,mn=-3
∴![]()
=![]()
=25+12
=37;
②解:∵m-n=5,![]()
∴![]()
∴![]()
![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列7个事件中:(1)掷一枚硬币,正面朝上.(2)从一副没有大小王的扑克牌中抽出一张恰为黑桃.(3)随意翻开一本有400页的书,正好翻到第100页.(4)天上下雨,马路潮湿.(5)你能长到身高4米.(6)买奖券中特等大奖.(7)掷一枚正方体骰子,得到的点数<7.其中(将序号填入题中的横线上即可)确定事件为________;不确定事件为________;不可能事件为________;必然事件为________;不确定事件中,发生可能性最大的是________,发生可能性最小的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在一次环保知识宣传活动中,需要印刷若干份调查问卷。印刷厂有甲、乙两种收费方式:甲种方式收制版费6元,每一份收印刷费0.1元;乙种方式不收制版费,每印一份收印刷费0.12元。设共印调查问卷![]() 份:
份:
(1)按甲种方式应收费多少元,按乙种方式应收费多少元(用含![]() 的代数式表示);
的代数式表示);
(2)若共需印刷500份调查问卷,通过计算说明选用哪种方式合算?
(3)印刷多少份调查问卷时,甲、乙两种方式收费一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
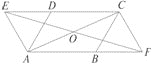
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果(不必写计算过程);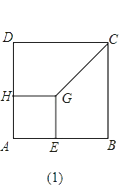
(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD:GC:EB;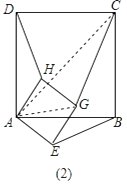
(3)把图(2)中的正方形都换成矩形,如图(3),且已知DA:AB=HA:AE=m:n,此时HD:GC:EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).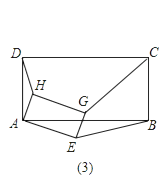
查看答案和解析>>
科目:初中数学 来源: 题型:
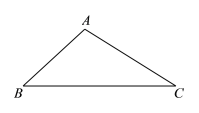
【题目】下面是小东设计的“作![]() 中
中![]() 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.
已知:![]() .
.
求作:![]() 中
中![]() 边上的高线
边上的高线![]() .
.
作法:如图,
①以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,以点
的长为半径作弧,以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 下方交于点
下方交于点![]() ;
;
②连接![]() 交
交![]() 于点
于点![]() .
.
所以线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ ![]() ,
, ![]() ,
,
∴点![]() ,
,![]() 分别在线段
分别在线段![]() 的垂直平分线上( )(填推理的依据).
的垂直平分线上( )(填推理的依据).
∴![]() 垂直平分线段
垂直平分线段![]() .
.
∴线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com