
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( ) 
A.5
B.4
C.![]()
D.![]()
【答案】D
【解析】解:如图,在等腰直角三角形△DEF中,∠EDF=90°,DE=DF,∠1=∠2=∠3, 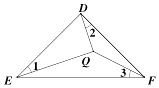
∵∠1+∠QEF=∠3+∠DFQ=45°,
∴∠QEF=∠DFQ,∵∠2=∠3,
∴△DQF∽△FQE,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵DQ=1,
∴FQ= ![]() ,EQ=2,
,EQ=2,
∴EQ+FQ=2+ ![]() ,
,
故选D
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对平行线的判定与性质的理解,了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( ) 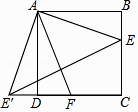
A.△AEE′是等腰直角三角形
B.AF垂直平分EE'
C.△E′EC∽△AFD
D.△AE′F是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是![]() .”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
.”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
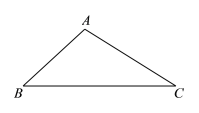
【题目】下面是小东设计的“作![]() 中
中![]() 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.
已知:![]() .
.
求作:![]() 中
中![]() 边上的高线
边上的高线![]() .
.
作法:如图,
①以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,以点
的长为半径作弧,以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 下方交于点
下方交于点![]() ;
;
②连接![]() 交
交![]() 于点
于点![]() .
.
所以线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ ![]() ,
, ![]() ,
,
∴点![]() ,
,![]() 分别在线段
分别在线段![]() 的垂直平分线上( )(填推理的依据).
的垂直平分线上( )(填推理的依据).
∴![]() 垂直平分线段
垂直平分线段![]() .
.
∴线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
2018年10月24日港珠澳大桥正式开通,它是中国建设史上里程最长、投资最多、施工难度最大的跨海桥梁项目,体现了我国逢山开路、遇水架桥的奋斗精神,体现了我国综合国力、自主创新能力,体现了我国勇创世界一流的民族志气. 港珠澳大桥全长55公里,跨越伶仃洋,东接香港特别行政区,西接广东省珠海市和澳门特别行政区,首次实现了珠海、澳门与香港的跨海陆路连接,极大地缩短了三地间的距离. 通车前,小亮妈妈驾车从香港到珠海的陆路车程大约220公里,如果行驶的平均速度不变,港珠澳大桥通车后,小亮妈妈驾车从香港到珠海所用的行驶时间比原来缩短了2小时15分钟,求小亮妈妈原来驾车从香港到珠海需要多长时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与应用.先填写下表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,则a= ;
=180,则a= ;
(3)拓展:已知![]() ,若
,若![]() ,则b= .
,则b= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com