练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将△ABC沿BC方向平移3cm得到△DEF，若△ABC的周长为20cm，则四边形ABFD的周长为________．

    【答案】26cm

    【解析】

    先根据平移的性质得DF=AC，AD=CF=3cm，再由△ABC的周长为20cm得到AB+BC+AC=20cm，然后利用等线段代换可计算出AB+BC+CF+DF+AD=26（cm），于是得到四边形ABFD的周长为26cm．

    ∵△ABC沿BC方向平移3cm得到△DEF，

    ∴DF=AC，AD=CF=3cm，

    ∵△ABC的周长为20cm，即AB+BC+AC=20cm，

    ∴AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=20+3+3=26（cm），

    即四边形ABFD的周长为26cm．

    故答案是：26cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算题
    （1）化简：（ ﹣ ）÷ +
    （2）计算：（﹣3）﹣2+ ﹣|1﹣2 |﹣（ ﹣3）0 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

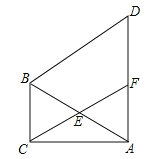
    【题目】如图，在△ABC中，∠ACB＝90°，∠CAB＝30°，以线段AB为边向外作等边△ABD，点E是线段AB的中点，连接CE并延长交线段AD于点F．

    （1）求证：四边形BCFD为平行四边形；

    （2）若AB＝6，求平行四边形BCFD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：y=y1+y2 ， y1与x成正比例，y2与x成反比例，当x=2时，y=﹣4；当x=﹣1时，y=5，求y与x的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】周末，小明坐公交车到滨海公园游玩，他从家出发0.8小时后达到中心书城，逗留一段时间后继续坐公交车到滨海公园，小明离家一段时间后，爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s（km）与小明离家时间t（h）的关系图，请根据图回答下列问题：

    （1）图中自变量是____，因变量是______；

    （2）小明家到滨海公园的路程为____ km，小明在中心书城逗留的时间为____ h；

    （3）小明出发______小时后爸爸驾车出发；

    （4）图中A点表示___________________________________；

    （5）小明从中心书城到滨海公园的平均速度为______km/h，小明爸爸驾车的平均速度为______km/h；（补充；爸爸驾车经过______追上小明）；

    （6）小明从家到中心书城时，他离家路程s与坐车时间t之间的关系式为________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BO、CO分别平分∠ABC、∠ACB．若∠BOC=110°，则∠A=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法错误的是（ ）

    A. 任意抛掷一个啤酒瓶盖，落地后印有商标一面向上的可能性大小是

    B. 一个转盘被分成8块全等的扇形区域，其中2块是红色，6块是蓝色. 用力转动转盘，当转盘停止后，指针对准红色区域的可能性大小是

    C. 一个不透明的盒子中装有2个白球，3个红球，这些球除颜色外都相同. 从这个盒子中随意摸出一个球，摸到白球的可能性大小是

    D. 100件同种产品中，有3件次品. 质检员从中随机取出一件进行检测，他取出次品的可能性大小是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ）
    A.5
    B.4
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

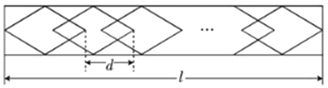
    【题目】学校植物园沿路护栏的纹饰部分准备设计成若干个形状、大小完全相同的四边形图案，每平移一个图案，纹饰长度就增加cm（如图）所示，已知每个四边形图案的水平方向的对角线长30cm．

    （1）若=26cm，且该纹饰要用231个四边形图案，求纹饰的长度；

    （2）当=20cm时，若保持（1）中纹饰长度不变，则需要多少个这样的四边形图案？

    查看答案和解析>>

    同步练习册答案