
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC.
(1)证明:BC=DE;
(2)若AC=12,求四边形ABCD的面积.

【答案】(1)见解析;(2) 72.
【解析】试题分析:(1)由等角角的余角相等求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE;(2)由全等三角形的性质得出S△ABC=S△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案.
试题解析:(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAC=∠EAD.
在△ABC和△ADE中, 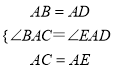 ,
,
∴△ABC≌△ADE(SAS).
∴BC=DE.
(2)∵△ABC≌△ADE ,
∴S△ABC=S△ADE,
∴S四边形ABCD=S△ABC+S△ACD=S△ADE+S△ACD=S△ACE=![]() ×122=72.
×122=72.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( ) 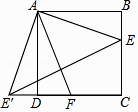
A.△AEE′是等腰直角三角形
B.AF垂直平分EE'
C.△E′EC∽△AFD
D.△AE′F是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作![]() 中
中![]() 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.
已知:![]() .
.
求作:![]() 中
中![]() 边上的高线
边上的高线![]() .
.
作法:如图,
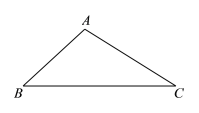
①以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,以点
的长为半径作弧,以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 下方交于点
下方交于点![]() ;
;
②连接![]() 交
交![]() 于点
于点![]() .
.
所以线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ ![]() ,
, ![]() ,
,
∴点![]() ,
,![]() 分别在线段
分别在线段![]() 的垂直平分线上( )(填推理的依据).
的垂直平分线上( )(填推理的依据).
∴![]() 垂直平分线段
垂直平分线段![]() .
.
∴线段![]() 是
是![]() 中
中![]() 边上的高线.
边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
2018年10月24日港珠澳大桥正式开通,它是中国建设史上里程最长、投资最多、施工难度最大的跨海桥梁项目,体现了我国逢山开路、遇水架桥的奋斗精神,体现了我国综合国力、自主创新能力,体现了我国勇创世界一流的民族志气. 港珠澳大桥全长55公里,跨越伶仃洋,东接香港特别行政区,西接广东省珠海市和澳门特别行政区,首次实现了珠海、澳门与香港的跨海陆路连接,极大地缩短了三地间的距离. 通车前,小亮妈妈驾车从香港到珠海的陆路车程大约220公里,如果行驶的平均速度不变,港珠澳大桥通车后,小亮妈妈驾车从香港到珠海所用的行驶时间比原来缩短了2小时15分钟,求小亮妈妈原来驾车从香港到珠海需要多长时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点(不与点
边上的一个动点(不与点![]() ,
,![]() 及
及![]() 中点重合),连接
中点重合),连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
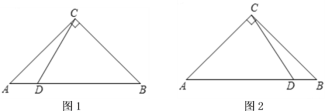
(1)如图1,当![]() 时,根据题意将图形补充完整,并直接写出
时,根据题意将图形补充完整,并直接写出![]() 的度数;
的度数;
(2)如图2,当![]() 时,用等式表示线段
时,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )

A.120°B.135°C.150°D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com