Question

【题目】如图，中，，，点为边上的一个动点(不与点，及中点重合)，连接，点关于直线的对称点为点，直线，交于点.

（1）如图1，当时，根据题意将图形补充完整，并直接写出的度数；

（2）如图2，当时，用等式表示线段，，之间的数量关系，并加以证明.

Answer 1

【答案】（1）（2）

【解析】

（1）作AH⊥CD延长于H，延长AH到E，使AH=HE，连接BE并延长BE，交CD延长线于F，可证明CF是AE的中垂线，即可得点E是点关于直线的对称点，根据中垂线的性质及等腰三角形的性质即可求出∠BFC的度数；（2）由点关于直线的对称点为点可得，即可证明，，，根据等腰三角形的性质可得，进而可得，由通过等量代换可知，在和Rt△ABC中，利用勾股定理即可证明结论.

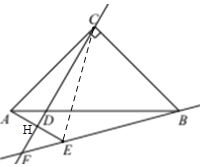
（1）如图：过点A作AH⊥CD延长于H，延长AH到E，使AH=HE，连接BE并延长BE，交CD延长线于F，

连接CE，

∵AH=EH，CH⊥AE，

∴CF是AE的中垂线，

∴点E是点关于直线的对称点，

∴图形即为所求.

∵CF是AE的中垂线，

∴AC=CE，

∵∠ACD=15°，

∴∠ACE=30°，∠FCE=15°，

∵∠ACB=90°，

∴∠ECB=60°，

∵AC=BC，

∴CE=BC，

∴∠CEB=60°，

∴∠BFC=∠CEB-∠FCE=60°-15°=45°.

（2）猜想：.

证明：连接，，延长，交于点，

∵点关于直线的对称点为点，

∴.

∴，，.

∵，

∴.

∴.

∴.

∵，

∴.

∴.

∴.

在中，.

∵在中，，

∴.

∴.