
【题目】选择适当的方法解下列方程:
(1)3(x+1)2=27; (2)2x2+6=7x;
(3)3x(x-2)=2(2-x); (4)y2-4y-3=0.
【答案】(1)x1=2,x2=-4.(2)x1=2,x2=![]() ;(3)x1=-
;(3)x1=-![]() ,x2=2;(4)y1=2+
,x2=2;(4)y1=2+![]() ,y2=2-
,y2=2-![]() .
.
【解析】(1)用直接开平方法解一元二次方程即可;
(2)用公式法解一元二次方程即可;
(2)用因式分解法解一元二次方程即可;
(4)用配方法解一元二次方程即可.
(1)原方程可化为(x+1)2=9,
∴x+1=±3,
∴x1=2,x2=-4.
(2)原方程可化2x2-7x+6=0,
a=2,b=-7,c=6,
b2-4ac=(-7)2-4×2×6=1>0,
∴x=![]() =
=![]() ,
,
∴x1=2,x2=![]() ;
;
(3)原方程可化为3x(x-2)-2(2-x)=0,
∴3x(x-2)+2(x-2)=0,
即(3x+2)(x-2)=0,
∴x1=-![]() ,x2=2;
,x2=2;
(4)原方程可化为y2-4y=3,
∴y2-4y+4=7,
∴(y-2)2=7,
∴y-2=±![]() ,
,
∴y1=2+![]() ,y2=2-
,y2=2-![]() .
.


科目:初中数学 来源: 题型:
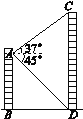
【题目】如图,从楼AB的A处测得对面楼CD的顶部C的仰角为37°,底部D的俯角为45°,两楼的水平距离BD为24 m,那么楼CD的高度约为________ m.(结果精确到1 m,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )

A.50B.62C.65D.68
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=3 cm,BC=4 cm,动点P从点B出发以2 cm/s的速度向点C移动,动点Q从点C出发以1 cm/s的速度向点A移动,当一点到达终点时,另一点也随之停止运动.若动点P,Q同时出发,则经过多少秒时,PQ∥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)解方程(x-1)2-5(x-1)+4=0时,我们发现:先将x-1看作一个整体,然后设x-1=y.……①,那么原方程可化为y2-5y+4=0,解得y1=1,y2=4.当y=1时,x-1=1,则x=2;当y=4时,x-1=4,则x=5,故原方程的解为x1=2,x2=5.
上述解题过程,在由原方程得到方程①的过程中,运用了“换元法”达到了解方程的目的,体现了转化的数学思想.
(解决问题)
(1)请利用以上知识解方程:(3x+5)2-4(3x+5)+3=0;
(2)在△ABC中,∠C=90°,两条直角边的长分别为a,b,斜边的长为c,且(a2+b2)(a2+b2+1)=12,求斜边c的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只蚂蚁从![]() 点出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为
点出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(1)蚂蚁离出发点最远时是多少厘米?是在出发点的左边还是右边?
(2)蚂蚁在爬行过程中,如果每爬行![]() 就得到1粒瓜子,那么最后它共得到多少粒瓜子?
就得到1粒瓜子,那么最后它共得到多少粒瓜子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:
在一个三角形中,如果一个角的度数是另一个角的度数![]() 倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为
倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为![]() ,
,![]() ,
,![]() 的三角形是“和谐三角形”
的三角形是“和谐三角形”
概念理解:
如图,![]() ,在射线
,在射线![]() 上找一点
上找一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为端点作射线
为端点作射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与
不与![]() 重合)
重合)

(1)![]() 的度数为 ,
的度数为 ,![]() (填“是”或“不是”)“和谐三角形”
(填“是”或“不是”)“和谐三角形”
(2)若![]() ,求证:
,求证:![]() 是“和谐三角形”.
是“和谐三角形”.
应用拓展:
如图,点![]() 在
在![]() 的边
的边![]() 上,连接
上,连接![]() ,作
,作![]() 的平分线
的平分线![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,
,![]() .若
.若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com