Question

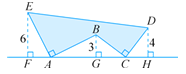
【题目】如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按图中所标注的数据，计算图中实线所围成的面积S是（ ）

A.50B.62C.65D.68

Answer 1

【答案】A

【解析】

由AE⊥AB，EF⊥FH，BG⊥AG，可以得到∠EAF=∠ABG，而AE=AB，∠EFA=∠AGB，由此可以证明△EFA≌△AGB，所以AF=BG，AG=EF；同理证得△BGC≌△CHD，GC=DH，CH=BG．故可求出FH的长，然后利用面积的割补法和面积公式即可求出图形的面积．

∵如图，AE⊥AB且AE=AB,EF⊥FH,BG⊥FH∠EAB=∠EFA=∠BGA=90，∠EAF+∠BAG=90，∠ABG+∠BAG=90∠EAF=∠ABG，

∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG△EFA≌△AGB，

∴AF=BG，AG=EF.

同理证得△BGC≌△CHD得GC=DH，CH=BG.

故FH=FA+AG+GC+CH=3+6+4+3=16

故S= (6+4)×163×46×3=50.

故选A.