
【题目】如图已知![]() ,
,![]() 为
为![]() 内一定点,
内一定点,![]() 上有一点
上有一点![]() ,
,![]() 上有一点
上有一点![]() ,当
,当![]() 的周长取最小值时,
的周长取最小值时,![]() 的度数是( )
的度数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
设点P关于OM、ON对称点分别为P′、P″,当点A、B在P′P″上时,△PAB周长为PA+AB+BP=P′P″,此时周长最小.根据轴对称的性质,可求出∠APB的度数.
分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A. B,
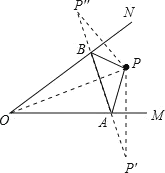
连接PA、PB,此时△PAB周长的最小值等于P′P″.
由轴对称性质可得,OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,
∴∠P′OP″=2∠MON=2×40°=80°,
∴∠OP′P″=∠OP'P′=(180°80°)÷2=50°
又∵∠BPO=∠OP″B=50°,∠APO=∠AP′O=50°,
∴∠APB=∠APO+∠BPO=100°.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )
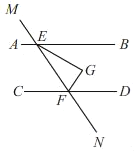
A. 20°B. 25°C. 35°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD=![]() AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的个数有( )
AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的个数有( )
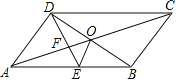
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
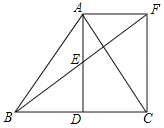
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代对于利用方程解决实际问题早有研究,《九章算术》中提到这么一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺:若将绳四折测之,绳多一尺.绳长、井深各几何?
这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺:如果将绳子折成四等份,那么每等份井外余绳一尺.问绳长和井深各多少尺?若设井深为x尺,则求解井深的方程正确的是( )
A.3(x+4)=4(x+1)B.3x+4=4x+1
C.![]() x+4=
x+4=![]() x+1D.
x+1D.![]() x﹣4=
x﹣4=![]() x﹣1
x﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数![]() ,定义一种新运算“
,定义一种新运算“![]() ”,规定
”,规定![]() .
.
(1)计算![]() 的值.
的值.
(2)当![]() 在数轴上的位置如图所示时,化简
在数轴上的位置如图所示时,化简![]() .
.
![]()
(3)当![]() 时,是否一定有
时,是否一定有![]() 或者
或者![]() ?若是,则说明理由;若不是,则举例说明.
?若是,则说明理由;若不是,则举例说明.
(4)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com