
【题目】对于有理数![]() ,定义一种新运算“
,定义一种新运算“![]() ”,规定
”,规定![]() .
.
(1)计算![]() 的值.
的值.
(2)当![]() 在数轴上的位置如图所示时,化简
在数轴上的位置如图所示时,化简![]() .
.
![]()
(3)当![]() 时,是否一定有
时,是否一定有![]() 或者
或者![]() ?若是,则说明理由;若不是,则举例说明.
?若是,则说明理由;若不是,则举例说明.
(4)已知![]() ,求
,求![]() 的值.
的值.
【答案】(1)6;(2)-2b;(3)不一定,理由见解析;(4)![]() 或-
或-![]() .
.
【解析】
(1)原式利用题中的新定义计算即可得到结果;
(2)根据数轴上点的位置判断出a+b与a-b的正负,利用绝对值的代数意义计算即可得到结果;
(3)当a⊙b=a⊙c时,不一定有b=c或者b=-c,举例即可;
(4)分类讨论a的正负,利用新定义将已知等式化简,即可求出a的值.
(1)根据题中的新定义得:2⊙(-3)=|2+(-3)|+|2-(-3)|=1+5=6;
(2)从a,b在数轴上的位置可得a+b<0,a-b>0,
∴a⊙b=|a+b|+|a-b|=-(a+b)+(a-b)=-2b;
(3)由a⊙b=a⊙c得:|a+b|+|a-b|=|a+c|+|a-c|,
不一定有b=c或者b=-c,
例如:取a=5,b=4,c=3,则|a+b|+|a-b|=|a+c|+|a-c|=10,
此时等式成立,但b≠c且b≠-c;
(4)当a≥0时,(a⊙a)⊙a=2a⊙a=4a=8+a,
解得:a=![]() ;
;
当a<0时,(a⊙a)⊙a=(-2a)⊙a=-4a=8+a,
解得:a=-![]() .
.
故a的值为:![]() 或-
或-![]() .
.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是( )
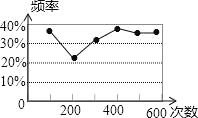
A. 袋子一定有三个白球
B. 袋子中白球占小球总数的十分之三
C. 再摸三次球,一定有一次是白球
D. 再摸1000次,摸出白球的次数会接近330次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由一些长度相等的小木棍组成的图形,图(1)(2)(3)需要的小木棍数量分别为3根、7根、15根,按照这种方式摆下去,第(4)个图形需要的木棍数量为__________,第(6)个图形需要的木棍数量为_________.
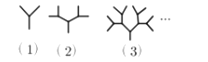
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为腰在AD的右侧作等腰直角
中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为腰在AD的右侧作等腰直角![]() ,∠DAE=90°,解答下列问题:
,∠DAE=90°,解答下列问题:
(1)如果AB=AC,∠BAC=90°
①如图1,当点D在线段BC上时(与点B不重合),线段CE、BD之间的位置关系为_______

②如图2,当点D在线段BC的延长线上时,①的结论是否仍然成立,如果不成立请说明理由,如果成立请加以证明

(2)如图3,如果AB≠AC,∠BAC≠90°,当点D在线段BC的延长线上时,试探究:
当∠ACB=45°时(点C与点E重合除外),求:∠ECA的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一口袋中装有四根长度分别为1 cm,3 cm,4 cm,5 cm的细木棒,小明手中有一根长度为3 cm的细木棒,现随机从口袋中取出两根细木棒与小明手中的细木棒放在一起,回答下列问题:
(1)求这三根细木棒能构成三角形的概率;
(2)求这三根细木棒能构成直角三角形的概率;
(3)求这三根细木棒能构成等腰三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,……,则第⑩个图形中棋子的颗数为__________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表列出了国外几个城市与北京的时差(带负号的数表示同一时刻比北京时间晚的时间):
城市 | 巴黎 | 东京 | 芝加哥 |
时差 |
|
|
|
![]() 如果现在的北京时间是下午
如果现在的北京时间是下午![]() 点,那么现在的芝加哥时间是多少?
点,那么现在的芝加哥时间是多少?
![]() 在
在![]() 的条件下,冬冬现在想给远在巴黎的父亲打电话,你认为合适吗?
的条件下,冬冬现在想给远在巴黎的父亲打电话,你认为合适吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.

(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com