
【题目】已知在![]() 中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为腰在AD的右侧作等腰直角
中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为腰在AD的右侧作等腰直角![]() ,∠DAE=90°,解答下列问题:
,∠DAE=90°,解答下列问题:
(1)如果AB=AC,∠BAC=90°
①如图1,当点D在线段BC上时(与点B不重合),线段CE、BD之间的位置关系为_______

②如图2,当点D在线段BC的延长线上时,①的结论是否仍然成立,如果不成立请说明理由,如果成立请加以证明

(2)如图3,如果AB≠AC,∠BAC≠90°,当点D在线段BC的延长线上时,试探究:
当∠ACB=45°时(点C与点E重合除外),求:∠ECA的度数?

【答案】(1)①CE⊥BD;②成立;证明见解析;(2)45°
【解析】
(1)①根据∠BAD=∠CAE,AB=AC,AD=AE,运用“SAS”证明![]() ,再利用全等三角形的性质即可得到线段CE、BD之间的关系;
,再利用全等三角形的性质即可得到线段CE、BD之间的关系;
②先根据“SAS”证明![]() ,再利用全等三角形的性质即可证得①中的结论仍然成立;
,再利用全等三角形的性质即可证得①中的结论仍然成立;
(2)过点A作FA⊥AC,交BC于点F, 根据“SAS”证明![]() ,再利用全等三角形的性质即可解决问题.
,再利用全等三角形的性质即可解决问题.
(1)CE⊥BD
∵AB=AC,∠BAC=90°
∴∠B=∠ACB=45°
∵等腰直角![]() ,∠DAE=90°
,∠DAE=90°
∴AD=AE
∴∠BAC-∠CAD=∠EAD-∠CAD
即∠BAD=∠CAE
在△ABD和△ACE中
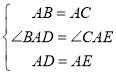
∴![]()
∴∠ACE=∠B=45°
∴∠BCE=∠ACB+∠ACE=90°
∴CE⊥BD
②答:①的结论仍然成立
证明:∵AB=AC,∠BAC=90°
∴∠B=∠ACB=45°
∵等腰直角![]() ,∠DAE=90°
,∠DAE=90°
∴AD=AE
∴∠BAC+∠CAD=∠EAD+∠CAD
即∠BAD=∠CAE
在△ABD和△ACE中
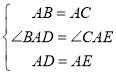
∴![]()
∴∠ACE=∠B=45°
∴∠BDE=∠ACB+∠ACE=90°
∴CE⊥BD
(2)
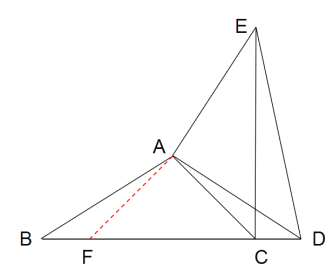
如图,解:作FA⊥AC,交BC于点F
∵∠ACB=45°
∴∠AFC=45°AF=AC
∵等腰直角![]() ,∠DAE=90°
,∠DAE=90°
∴AD=AE,∠ADE=∠AED=45°
∵∠FAC=∠DAE=90°
∴∠FAC+∠CAD=∠DAE+∠CAD
即∠FAD=∠CAE
在△FAD和△CAE中
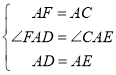
∴![]()
∴∠ECA=∠AFC=45°


科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() ,对角线
,对角线![]() 交于点
交于点![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
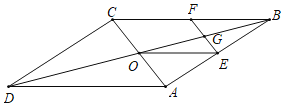
(1)证明:四边形![]() 是平行四边形
是平行四边形
(2)点![]() 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把1,2,3,4......按下列方式排列:
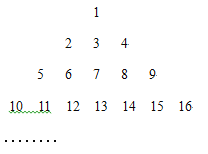
(1)按照这样的排列,第8行的最后一个数是 ,这个数的平方根是 ;正中间一列,自上而下第![]() 个数是 (用
个数是 (用![]() 表示);
表示);
(2)求第15行所有数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张质地相同并标有数字0,1,2,3的卡片(如图所示),将卡片洗匀后,背面朝上放在桌面上,第一次任意抽取一张(不放回),第二次再抽一张.用列表法或画树状图法求两次所抽卡片上的数字恰好是方程x2-5x+6=0的两根的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数![]() ,定义一种新运算“
,定义一种新运算“![]() ”,规定
”,规定![]() .
.
(1)计算![]() 的值.
的值.
(2)当![]() 在数轴上的位置如图所示时,化简
在数轴上的位置如图所示时,化简![]() .
.
![]()
(3)当![]() 时,是否一定有
时,是否一定有![]() 或者
或者![]() ?若是,则说明理由;若不是,则举例说明.
?若是,则说明理由;若不是,则举例说明.
(4)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A,B,C,D四张卡片,其正面分别写有“、寸、又、日”,有的能独立成字,有的能组合成字.现四张卡片背面朝上.
(1)任意翻过一张卡片,能独立成字的概率为________;
(2)先任意翻过一张卡片作为左部偏旁,再任意翻过一张与其组合,请用列表或画树状图的方法求翻过的两张卡片恰好能组合成字的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
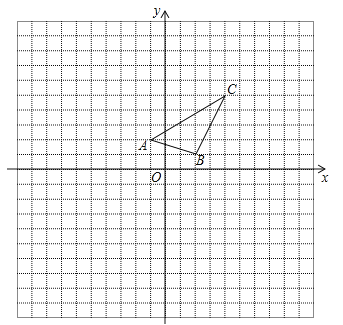
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com