
【题目】有四张质地相同并标有数字0,1,2,3的卡片(如图所示),将卡片洗匀后,背面朝上放在桌面上,第一次任意抽取一张(不放回),第二次再抽一张.用列表法或画树状图法求两次所抽卡片上的数字恰好是方程x2-5x+6=0的两根的概率.
![]()
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
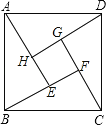
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
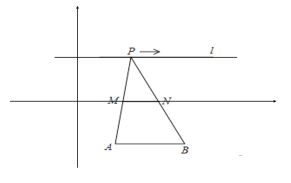
【题目】如图,在直角坐标系中,点![]() ,
,![]() 为定点,A(2,-3),B(4,-3),定直线
为定点,A(2,-3),B(4,-3),定直线![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() 到AB的距离为6,
到AB的距离为6,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,对下列各值:①线段
的中点,对下列各值:①线段![]() 的长度始终为1;②
的长度始终为1;②![]() 的周长固定不变;③
的周长固定不变;③![]() 的面积固定不变;④若存在点Q使得四边形APBQ是平行四边形,则Q到
的面积固定不变;④若存在点Q使得四边形APBQ是平行四边形,则Q到![]() 所在的直线的距离必为9;其中说法正确的是__(填序号)
所在的直线的距离必为9;其中说法正确的是__(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
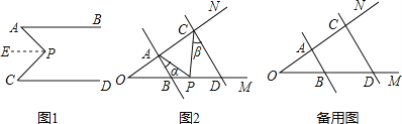
【题目】(1)如图1,AB∥CD,∠A=35°,∠C=40°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() = ; (2)
= ; (2)![]() = ; (3)
= ; (3)![]() ;
;
(4)![]() ; (5)
; (5)![]() ; (6)a3·a3= ;
; (6)a3·a3= ;
(7) (x3)5= ; (8)(-2x2y3)3= ; (9) (x-y)6÷(x-y)3= ;
(10)a2b(ab-4b2) (11)(2a-3b)(2a+5b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为腰在AD的右侧作等腰直角
中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为腰在AD的右侧作等腰直角![]() ,∠DAE=90°,解答下列问题:
,∠DAE=90°,解答下列问题:
(1)如果AB=AC,∠BAC=90°
①如图1,当点D在线段BC上时(与点B不重合),线段CE、BD之间的位置关系为_______

②如图2,当点D在线段BC的延长线上时,①的结论是否仍然成立,如果不成立请说明理由,如果成立请加以证明

(2)如图3,如果AB≠AC,∠BAC≠90°,当点D在线段BC的延长线上时,试探究:
当∠ACB=45°时(点C与点E重合除外),求:∠ECA的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
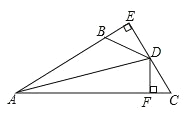
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
查看答案和解析>>
科目:初中数学 来源: 题型:
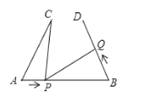
【题目】如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA=60 ,点 P 在线段 AB 上以 1cm/s 的速度由点A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动。它们运动的时间为 t(s),则点 Q的运动速度为________cm/s,使得 A. C. P 三点构成的三角形与 B. P、Q 三点构成的三角形全等。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com